
題目列表(包括答案和解析)
設函數f(x)= 在[1,+∞
在[1,+∞ 上為增函數.
上為增函數.
(1)求正實數a的取值范圍;
(2)比較 的大小,說明理由;
的大小,說明理由;
(3)求證: (n∈N*, n≥2)
(n∈N*, n≥2)
【解析】第一問中,利用
解:(1)由已知: ,依題意得:
,依題意得: ≥0對x∈[1,+∞
≥0對x∈[1,+∞ 恒成立
恒成立
∴ax-1≥0對x∈[1,+∞ 恒成立 ∴a-1≥0即:a≥1
恒成立 ∴a-1≥0即:a≥1
(2)∵a=1 ∴由(1)知:f(x)= 在[1,+∞)上為增函數,
在[1,+∞)上為增函數,
∴n≥2時:f( )=
)=
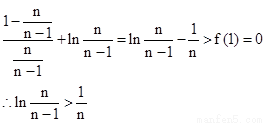
(3) ∵ ∴
∴
已知橢圓
 的離心率為
的離心率為 ,以原點為圓心,橢圓的短半軸長為半徑的圓與直線
,以原點為圓心,橢圓的短半軸長為半徑的圓與直線 相切.
相切.
(I)求橢圓 的方程;
的方程;
(II)若過點 (2,0)的直線與橢圓
(2,0)的直線與橢圓 相交于兩點
相交于兩點 ,設
,設 為橢圓上一點,且滿足
為橢圓上一點,且滿足 (O為坐標原點),當
(O為坐標原點),當 <
< 時,求實數
時,求實數 的取值范圍.
的取值范圍.
【解析】本試題主要考查了橢圓的方程以及直線與橢圓的位置關系的運用。
第一問中,利用
第二問中,利用直線與橢圓聯系,可知得到一元二次方程中 ,可得k的范圍,然后利用向量的
,可得k的范圍,然后利用向量的 <
< 不等式,表示得到t的范圍。
不等式,表示得到t的范圍。
解:(1)由題意知

學校要用三輛車從北湖校區把教師接到文廟校區,已知從北湖校區到文廟校區有兩條公路,汽車走公路①堵車的概率為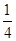 ,不堵車的概率為
,不堵車的概率為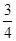 ;汽車走公路②堵車的概率為
;汽車走公路②堵車的概率為 ,不堵車的概率為
,不堵車的概率為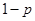 ,若甲、乙兩輛汽車走公路①,丙汽車由于其他原因走公路②,且三輛車是否堵車相互之間沒有影響。(I)若三輛車中恰有一輛車被堵的概率為
,若甲、乙兩輛汽車走公路①,丙汽車由于其他原因走公路②,且三輛車是否堵車相互之間沒有影響。(I)若三輛車中恰有一輛車被堵的概率為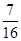 ,求走公路②堵車的概率;(Ⅱ)在(I)的條件下,求三輛車中被堵車輛的個數
,求走公路②堵車的概率;(Ⅱ)在(I)的條件下,求三輛車中被堵車輛的個數 的分布列和數學期望。
的分布列和數學期望。
【解析】第一問中,由已知條件結合n此獨立重復試驗的概率公式可知,得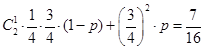
第二問中 可能的取值為0,1,2,3
可能的取值為0,1,2,3 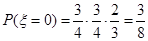 ,
, 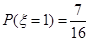
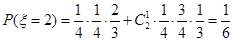 ,
,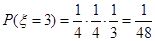
從而得到分布列和期望值
解:(I)由已知條件得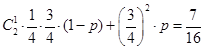 ,即
,即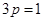 ,則
,則 的值為
的值為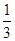 。
。
(Ⅱ) 可能的取值為0,1,2,3
可能的取值為0,1,2,3 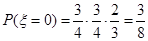 ,
, 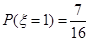
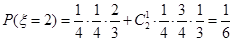 ,
,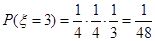
 的分布列為:(1分)
的分布列為:(1分)
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
所以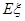
 某公司推出了一種高效環保型洗滌用品,年初上市后,公司經歷了從虧損到盈利的過程,下面的二次函數圖象(部分)刻畫了該公司年初以來累積利潤s(萬元)與銷售時間t(月)之間的關系(即前t個月的利潤總和s與t之間的關系).根據圖象提供的信息解答下列問題:
某公司推出了一種高效環保型洗滌用品,年初上市后,公司經歷了從虧損到盈利的過程,下面的二次函數圖象(部分)刻畫了該公司年初以來累積利潤s(萬元)與銷售時間t(月)之間的關系(即前t個月的利潤總和s與t之間的關系).根據圖象提供的信息解答下列問題:| 10-x |
| 10+x |
| 10-x |
| 10+x |
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com