
題目列表(包括答案和解析)
已知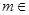 R,函數
R,函數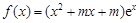 .
.
⑴若函數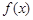 沒有零點,求實數
沒有零點,求實數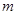 的取值范圍;
的取值范圍;
⑵若函數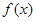 存在極大值,并記為
存在極大值,并記為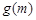 ,求
,求 的表達式;
的表達式;
⑶當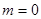 時,求證:
時,求證: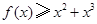 .
.
【解析】(1)求導研究函數f(x)的最值,說明函數f(x)的最大值<0,或f(x)的最小值>0.
(2)根據第(1)問的求解過程,直接得到g(m).
(3)構造函數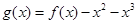 ,證明
,證明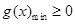 即可,然后利用導數求g(x)的最小值.
即可,然后利用導數求g(x)的最小值.
 ,x∈(0,+∞)的最小值,并確定取得最小值時x的值.列表如下:
,x∈(0,+∞)的最小值,并確定取得最小值時x的值.列表如下:| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
 (x>0)在區間(0,2)上遞減;
(x>0)在區間(0,2)上遞減; (x>0)在區間________上遞增.
(x>0)在區間________上遞增. (x>0)在區間(0,2)遞減.
(x>0)在區間(0,2)遞減. (x<0)有沒有最值?如果有,請說明是最大值還是最小值,以及取相應最值時x的值.
(x<0)有沒有最值?如果有,請說明是最大值還是最小值,以及取相應最值時x的值. ,(a<0,b<0)在區間________ 和________上單調遞增.
,(a<0,b<0)在區間________ 和________上單調遞增.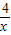 ,x∈(0,+∞)的最小值,并確定取得最小值時x的值.列表如下:
,x∈(0,+∞)的最小值,并確定取得最小值時x的值.列表如下:| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
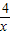 (x>0)在區間(0,2)上遞減;
(x>0)在區間(0,2)上遞減;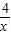 (x>0)在區間______上遞增.
(x>0)在區間______上遞增.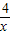 (x>0)在區間(0,2)遞減.
(x>0)在區間(0,2)遞減.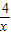 (x<0)有沒有最值?如果有,請說明是最大值還是最小值,以及取相應最值時x的值.
(x<0)有沒有最值?如果有,請說明是最大值還是最小值,以及取相應最值時x的值.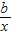 ,(a<0,b<0)在區間______
,(a<0,b<0)在區間______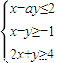 時,z=x+y( )
時,z=x+y( )| 4x+a |
| x2+1 |
| 12 |
| 5 |
| 12 |
| 25 |
| 2 |
| x |
| 8 |
| 5 |
一. 填空題(每題4分,共48分)
1. {0}; 2. 四; 3. 12; 4. 0; 5. 4; 6. 理 、文7; 7. 理
、文7; 7. 理
 ; 12.
; 12.
 (或
(或 ).
).
二.選擇題(每題4分,共16分)
13.D; 14.B; 15.C; 16.理B、文B.
三. 解答題. 17.(本題滿分12分)解:由已知得 (3分)
(3分)
∴ , ∴
, ∴ (6分)
(6分)
∴ 又
又 ,即
,即 ,∴
,∴ (9分)
(9分)
∴ 的面積S=
的面積S= .
(12分)
.
(12分)
18.(本題滿分12分)解:∵ ,∴
,∴ (5分)
(5分)
∵ ,欲使
,欲使 是純虛數,
是純虛數,
而 =
= (7分)
(7分)
∴ , 即
, 即 (11分)
(11分)
∴當 時,
時, 是純虛數.
(12分)
是純虛數.
(12分)
19.(本題滿分14分,第1小題滿分9分,第2小題滿分5分)
解:(1)依題意設 ,則
,則 ,
(2分)
,
(2分)
 (4分) 而
(4分) 而 ,
,
∴ ,即
,即 , (6分) ∴
, (6分) ∴ (7分)
(7分)
從而 .
(9分)
.
(9分)
(2) 平面
平面 ,
,
∴直線 到平面
到平面 的距離即點
的距離即點 到平面
到平面 的距離
(2分)
的距離
(2分)
也就是 的斜邊
的斜邊 上的高,為
上的高,為 .
(5分)
.
(5分)
20.(本題滿分14分,第1小題滿分8分,第2小題滿分6分)
解:(1)不正確.
(2分)
沒有考慮到 還可以小于
還可以小于 .
(3分)
.
(3分)
正確解答如下:
令 ,則
,則 ,
,
當 時,
時, ,即
,即 (5分)
(5分)
當 時,
時, ,即
,即 (7分)
(7分)
∴ 或
或 ,即
,即 既無最大值,也無最小值.
(8分)
既無最大值,也無最小值.
(8分)
(2)(理)對于函數 ,令
,令
①當 時,
時, 有最小值,
有最小值, ,
(9分)
,
(9分)
當 時,
時, ,即
,即 ,當
,當 時,即
時,即
∴ 或
或 ,即
,即 既無最大值,也無最小值.
(10分)
既無最大值,也無最小值.
(10分)
②當 時,
時, 有最小值,
有最小值, ,
,
此時, ,∴
,∴ ,即
,即 ,
, 既無最大值,也無最小值 .(11分)
既無最大值,也無最小值 .(11分)
③當 時,
時, 有最小值,
有最小值, ,即
,即 (12分)
(12分)
∴ ,即
,即 ,
,
∴當 時,
時, 有最大值
有最大值 ,沒有最小值.
(13分)
,沒有最小值.
(13分)
∴當 時,
時, 既無最大值,也無最小值。
既無最大值,也無最小值。
當 時,
時, 有最大值
有最大值 ,此時
,此時 ;沒有最小值.
(14分)
;沒有最小值.
(14分)
(文)∵ , ∴
, ∴ (12分)
(12分)
∴函數 的最大值為
的最大值為 (當
(當 時)而無最小值. (14分)
時)而無最小值. (14分)
21.(本滿分16分,第1、2小題滿分各4分,第3小題滿分8分)
解:(1) (4分)
(4分)
(2)由 解得
解得 (7分)
(7分)
所以第 個月更換刀具.
(8分)
個月更換刀具.
(8分)
(3)第 個月產生的利潤是:
個月產生的利潤是: (9分)
(9分)
 個月的總利潤:
個月的總利潤: (11分)
(11分)
 個月的平均利潤:
個月的平均利潤: (13分)
(13分)
由  且
且
在第7個月更換刀具,可使這7個月的平均利潤 最大(13.21萬元) (14分)此時刀具厚度為
最大(13.21萬元) (14分)此時刀具厚度為 (mm)
(16分)
(mm)
(16分)
22.(本題滿分18分,第1、2小題滿分各4分,第3小題滿分10分)
解:(1) (4分)
(4分)
(2)各點的橫坐標為: (8分)
(8分)
(3)過 作斜率為
作斜率為 的直線
的直線 交拋物線于另一點
交拋物線于另一點 ,
(9分)
,
(9分)
則一般性的結論可以是:
點 的相鄰橫坐標之和構成以
的相鄰橫坐標之和構成以 為首項和公比的等比數列(或:點
為首項和公比的等比數列(或:點 無限趨向于某一定點,且其橫(縱)坐標之差成等比數列;或:
無限趨向于某一定點,且其橫(縱)坐標之差成等比數列;或: 無限趨向于某一定點,且其橫(縱)坐標之差成等比數列,等)(12分)
無限趨向于某一定點,且其橫(縱)坐標之差成等比數列,等)(12分)
證明:設過點 作斜率為
作斜率為 的直線交拋物線于點
的直線交拋物線于點 由
由
 得
得 或
或 ;
;
 點
點 的橫坐標為
的橫坐標為 ,則
,則 (14分)
(14分)
于是 兩式相減得:
兩式相減得: (16分)
(16分)


=

故點 無限逼近于點
無限逼近于點
同理 無限逼近于點
無限逼近于點 (18分)
(18分)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com