
題目列表(包括答案和解析)
(15分)已知 是數列
是數列 的前
的前 項和,
項和, (
( ,
, ),且
),且 .
.
(1)求 的值,并寫出
的值,并寫出 和
和 的關系式;
的關系式;
(2)求數列 的通項公式及
的通項公式及 的表達式;
的表達式;
(3)我們可以證明:若數列 有上界(即存在常數
有上界(即存在常數 ,使得
,使得 對一切
對一切 恒成立)且單調遞增;或數列
恒成立)且單調遞增;或數列 有下界(即存在常數
有下界(即存在常數 ,使得
,使得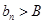 對一切
對一切 恒成立)且單調遞減,則
恒成立)且單調遞減,則 存在.直接利用上述結論,證明:
存在.直接利用上述結論,證明: 存在.
存在.
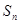 是數列
是數列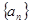 的前
的前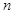 項和,
項和,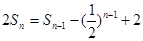 (
(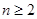 ,
,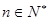 ),且
),且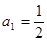 .
.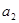 的值,并寫出
的值,并寫出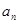 和
和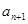 的關系式;
的關系式;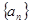 的通項公式及
的通項公式及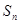 的表達式;
的表達式; 3)我們可以證明:若數列
3)我們可以證明:若數列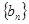 有上界(即存在常數
有上界(即存在常數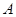 ,使得
,使得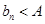 對一切
對一切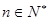 恒成立)且單調遞增;或數列
恒成立)且單調遞增;或數列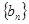 有下界(即存在常數
有下界(即存在常數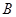 ,使得
,使得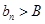 對一切
對一切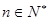 恒成立)且單調遞減,則
恒成立)且單調遞減,則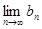 存在.直接利用上述結論,證明:
存在.直接利用上述結論,證明: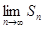 存在.
存在.  (n≥2,n∈N*),且
(n≥2,n∈N*),且 .
.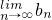 存在.直接利用上述結論,證明:
存在.直接利用上述結論,證明: 存在.
存在.已知Sn是數列{an}的前n項和,![]() (
(![]() ,
,![]() ),且
),且![]() .
.
(1)求a2的值,并寫出an和an+1的關系式;
(2)求數列{an}的通項公式及Sn的表達式;
(3)我們可以證明:若數列{bn}有上界(即存在常數A,使得bn<A對一切n∈N*恒成立)且單調遞增;或數列{bn}有下界(即存在常數B,使得bn>B對一切n∈N*恒成立)且單調遞減,則![]() 存在.直接利用上述結論,證明:
存在.直接利用上述結論,證明:![]() 存在.
存在.
已知公比為![]() 的等比數列{
的等比數列{![]() }是遞減數列,且滿足
}是遞減數列,且滿足![]() +
+![]() +
+![]() =
=![]() ,
,![]()
![]()
![]() =
=![]()
(I)求數列{![]() }的通項公式;
}的通項公式;
(II)求數列{![]() }的前
}的前![]() 項和為
項和為![]() ;
;
(Ⅲ)若![]() ,證明:
,證明:![]() ≥
≥![]() .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com