
題目列表(包括答案和解析)
 (本小題滿分12分)如圖,已知直三棱柱ABC—A1B1C1的側棱長為2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中點. (Ⅰ)求異面直線AB和C1D所成的角(用反三角函數表示);(Ⅱ)若E為AB上一點,試確定點E在AB上的位置,使得A1E⊥C1D;
(本小題滿分12分)如圖,已知直三棱柱ABC—A1B1C1的側棱長為2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中點. (Ⅰ)求異面直線AB和C1D所成的角(用反三角函數表示);(Ⅱ)若E為AB上一點,試確定點E在AB上的位置,使得A1E⊥C1D;
(Ⅲ)在(Ⅱ)的條件下,求點D到平面B1C1E的距離.
(本小題滿分12分)
如圖,在三棱柱ADF—BCE中,側棱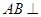 底面
底面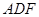 ,底面
,底面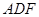 是等腰直角三角形,且
是等腰直角三角形,且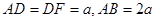 ,M、G分別是AB、DF的中點.
,M、G分別是AB、DF的中點.
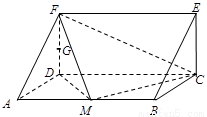
(1)求證GA∥平面FMC;
(2)求直線DM與平面ABEF所成角。
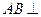 底面
底面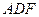 ,底面
,底面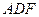 是等腰直角三角形,且
是等腰直角三角形,且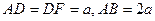 ,M、G分別是AB、DF的中點.
,M、G分別是AB、DF的中點. 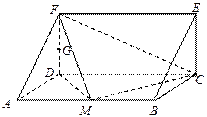
(本小題滿分12分)
已知橢圓的中心在原點,焦點在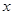 軸上,長軸長是短軸長的2倍且經過點M(2,1),平行于OM的直線
軸上,長軸長是短軸長的2倍且經過點M(2,1),平行于OM的直線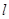 在
在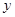 軸上的截距為
軸上的截距為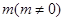 ,
,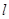 交橢圓于A、B兩個不同點.
交橢圓于A、B兩個不同點.
(1)求橢圓的方程;
(2)求m的取值范圍;
(3)求證直線MA、MB與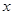 軸始終圍成一個等腰三角形.
軸始終圍成一個等腰三角形.
(本小題滿分12分)已知橢圓的中心在原點,焦點在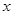 軸上,離心率為
軸上,離心率為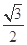 ,且經過點
,且經過點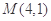 ,直線
,直線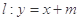 交橢圓于不同的兩點
交橢圓于不同的兩點 .
.
(1)求橢圓的方程;
(2)求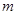 的取值范圍;
的取值范圍;
(3)若直線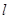 不過點
不過點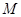 ,求證:直線
,求證:直線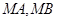 與
與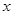 軸圍成一個等腰三角形.
軸圍成一個等腰三角形.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com