題目列表(包括答案和解析)
| 24 | 5 |
| 2 |
天津精通高考復讀學校數學教研組組長 么世濤
一、選擇題 ：1-4， BBBB ；5-8，DABD。
提示：1.
2.
3.用
代替
得
4．
5.
,
或
6.
7．略
8．
二、填空題：9.60； 10. 15：10：20 ； 11.
； 12.
；
13.0.74 ； 14. ①、
；②、圓；③.
提示：
9.
10．
，
，
11．
，
12．
，
，
，
，
13．
14．略
三、解答題
15. 解：(1)
.
(2)設抽取
件產品作檢驗，則
，
，得：
，即 
故至少應抽取8件產品才能滿足題意.
16. 解：由題意得
，
，原式可化為
,
而
,
故原式=
.
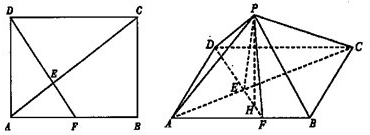
17. 解：(1)顯然
，連接
，∵
，
，
∴
.由已知
，∴
，
.
∵
∽
， 
，
∴
即 
.
∴
.
(2) 
當且僅當
時，等號成立.此時
，即
為
的中點.于是由
，知平面
，
是其交線，則過
作
。
∴
就是
與平面
所成的角.由已知得
，
，
∴
， 
, 
.
(3) 設三棱錐
的內切球半徑為
，則
∵
，
，
，
，
，
∴
.
18. 解： (1) 
，
(2) ∵ 
，
∴當
時，
∴當
時，
，
∵
,
,
,
.
∴ 
的最大值為
或
中的最大者．
∵ 
∴ 當
時，有最大值為
．
19.(1)解：∵函數
的圖象過原點，
∴
即
，
∴
.
又函數
的圖象關于點
成中心對稱，
∴
，
.
(2)解：由題意有
即
，
即
，即
.
∴數列{
}是以1為首項，1為公差的等差數列.
∴
，即
. ∴
.
∴ 
，
，
，.
(3)證明：當
時，
故 
20. (1)解：∵
，又
，
∴
.
又∵
，且
∴ 
.
(2)解：由，，猜想
(3)證明：用數學歸納法證明：
①當
時，，猜想正確；
②假設
時，猜想正確，即
1°若
為正奇數，則
為正偶數，
為正整數，
2°若為正偶數，則
為正整數，
，又
，且
所以
即當
時，猜想也正確
由①，②可知，成立.
（二）
一、1-4，AABB,5-8,CDCB；
提示： 1. 
即 
2． 
即 
3． 
即
，也就是 
，
4．先確定是哪兩個人的編號與座位號一致，有
種情況，如編號為1的人坐1號座位，且編號為2的人坐2號座位有以下情形：
|
，又
，所以
，且
，所以
，原文對應的數字是12，對應的字母是
；
；
； 10.2；11.-48； 12. 
； 13、5； 14、①3，②
，③
，
，
是首相為
的等差數列，于是
又
，所以
，
，
。
，
，所以
同解于
。
，又根據相交弦定理DF?EF＝BF?AF
，從而
QF， ∴
∴
又 
所以 
的值域為
。
，飛機B能安全飛行的概率為
，則
所以 
時，
，
，
；
時，
，
，
；
時，
，
，
；
,則
，
，
，
，
，所以 
，也就是
，所以 
，即
。
(當且僅當
取等號)
分別為
的中點，于是 
，
。
，所以 
，
是平面
的一個法向量，則
也就是
是平面
的一個法向量，
所以 
即 
是等差數列。
即 
(
)
所以 
是增函數，僅須 
或