
題目列表(包括答案和解析)
|
A、
| ||
B、
| ||
C、
| ||
D、
|
| x | 1+ex |
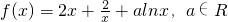 .
.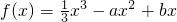 .(a,b∈R)
.(a,b∈R)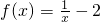 .
.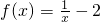 在(0,+∞)上是減函數.
在(0,+∞)上是減函數.一、選擇題:
1、A 2、B 3、A 4、D 5、D 6、C7、A 8、C9、A10、C 11、A 12、B
二、填空題:
13、 {1,2,3} 14、 充分而不必要條件 15、 2 16、.files/image040.gif) 17、 48
17、 48
18、 4 19、.files/image279.gif) 20、
20、.files/image281.gif) 21、4 22、
21、4 22、.files/image283.gif)
23、.files/image285.gif) 24、
24、.files/image287.gif) 25、
25、.files/image289.gif) 26、①②
26、①②
三、解答題:
27解:由題設,當.files/image291.gif) 時,
時,.files/image293.gif)
.files/image295.gif)
由題設條件可得.files/image297.gif)
.files/image299.gif)
(2)由(1)當.files/image301.gif)
這時數列.files/image303.gif) =
=.files/image305.gif)
.files/image307.gif)
這時數列.files/image309.gif) ①
①
上式兩邊同乘以.files/image311.gif) ,得
,得
.files/image313.gif) ②
②
①―②得
.files/image315.gif)
=.files/image317.gif)
所以.files/image319.gif)
28解:(1)因BC∥B
且B.files/image321.gif) 平面MNB1, BC
平面MNB1, BC.files/image323.gif) 平面MNB1,
平面MNB1,
故BC∥平面MNB1.
(2)因BC⊥AC,且ABC-A1B
故BC⊥平面ACC
因BC.files/image321.gif) 平面A1CB,
平面A1CB,
故平面A1CB⊥平面ACC
29解:設.files/image325.gif) 延長
延長.files/image327.gif) 交
交.files/image329.gif) 于
于.files/image097.gif)
.files/image332.gif)
.files/image334.gif)
.files/image336.gif)
.files/image338.gif)
.files/image340.gif)
.files/image230.gif)
.files/image342.gif)
令.files/image344.gif)
.files/image346.gif) -10
-10
故當.files/image348.gif) 時,S的最小值為
時,S的最小值為.files/image350.gif) ,當
,當.files/image352.gif) 時 S 的
時 S 的.files/image354.gif)
30解:.files/image356.gif)
點.files/image358.gif)
∴圓心.files/image360.gif)
(2)由直線.files/image362.gif)
∴設.files/image364.gif)
將直線.files/image366.gif) 代人圓方程
代人圓方程
得.files/image368.gif)
.files/image370.gif)
得.files/image372.gif)
由韋達定理得.files/image374.gif)
.files/image376.gif)
又.files/image378.gif) ∴
∴.files/image380.gif)
即.files/image382.gif)
解得.files/image384.gif)
∴所求直線方程為.files/image386.gif)
31解:(1)當a=1時,.files/image388.gif) ,其定義域是
,其定義域是.files/image390.gif) ,
,
.files/image392.gif)
令.files/image394.gif) ,即
,即.files/image396.gif) ,解得
,解得.files/image398.gif) 或
或.files/image400.gif) .
.
.files/image402.gif) ,
,.files/image404.gif) 舍去.
舍去.
當.files/image406.gif) 時,
時,.files/image408.gif) ;當
;當.files/image137.gif) 時,
時,.files/image411.gif) .
.
∴函數.files/image033.gif) 在區間(0,1)上單調遞增,在區間(1,+∞)上單調遞減
在區間(0,1)上單調遞增,在區間(1,+∞)上單調遞減
∴當x=1時,函數.files/image033.gif) 取得最大值,其值為
取得最大值,其值為.files/image414.gif) .
.
當.files/image416.gif) 時,
時,.files/image418.gif) ,即
,即.files/image420.gif) .
.
∴函數.files/image033.gif) 只有一個零點.
只有一個零點.
(2)法一:因為.files/image422.gif) 其定義域為
其定義域為.files/image390.gif) ,
,
所以.files/image425.gif)
①當a=0時,.files/image427.gif) 在區間
在區間.files/image390.gif) 上為增函數,不合題意
上為增函數,不合題意
②當a>0時,.files/image430.gif) 等價于
等價于.files/image432.gif) ,即
,即.files/image434.gif) .
.
此時.files/image033.gif) 的單調遞減區間為
的單調遞減區間為.files/image437.gif) .
.
依題意,得.files/image439.gif) 解之得
解之得.files/image441.gif) .
.
③當a<0時,.files/image430.gif) 等價于
等價于.files/image444.gif) ,即
,即.files/image446.gif) ?
?
此時.files/image033.gif) 的單調遞減區間為
的單調遞減區間為.files/image449.gif) ,
,.files/image451.gif) 得
得.files/image453.gif)
綜上,實數a的取值范圍是.files/image455.gif)
法二:.files/image457.gif)
.files/image459.gif)
由.files/image033.gif) 在區間
在區間.files/image462.gif) 上是減函數,可得
上是減函數,可得
.files/image464.gif) 在區間
在區間.files/image462.gif) 上恒成立.
上恒成立.
① 當.files/image467.gif) 時,
時,.files/image469.gif) 不合題意
不合題意
② 當.files/image471.gif) 時,可得
時,可得.files/image473.gif) 即
即.files/image475.gif)
.files/image477.gif)
.files/image479.gif)
32解:(1) 由 .files/image481.gif) 得
得.files/image483.gif)
.files/image485.gif)
.files/image487.gif)
(2) .files/image489.gif)
.files/image491.gif)
.files/image493.gif)
.files/image495.gif)
.files/image497.gif) 又
又 .files/image499.gif)
.files/image495.gif) 數列
數列.files/image273.gif) 是一個首項為
是一個首項為
.files/image502.gif) ,公比為2的等比數列;
,公比為2的等比數列;
.files/image495.gif)
.files/image504.gif)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com