年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image145.jpg)
故當(dāng)年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image151.gif) 時,
時,
年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image153.gif)
三、解答題:
15.解:(Ⅰ)由題可知函數(shù)定義域關(guān)于原點對稱.
當(dāng)年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image155.gif) ,
,
則年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image157.gif) ,
,
∴年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image159.gif)
當(dāng)年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image161.gif)
則年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image163.gif) ,
,
∴年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image159.gif)
綜上所述,對于年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image165.gif) ,∴函數(shù)
,∴函數(shù)年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image044.gif) 是偶函數(shù).
是偶函數(shù).
(Ⅱ)當(dāng)x>0時,年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image168.gif) ,
,
設(shè)年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image170.gif)
當(dāng)年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image172.gif)
∴函數(shù)年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image174.gif) 上是減函數(shù),函數(shù)
上是減函數(shù),函數(shù)年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image176.gif) 上是增函數(shù).
上是增函數(shù).
(另證:當(dāng)年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image178.gif) ;
;
∵年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image180.gif)
年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image182.gif)
∴函數(shù)年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image174.gif) 上是減函數(shù),在
上是減函數(shù),在年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image184.gif) 上是增函數(shù).
上是增函數(shù).
16.解:(Ⅰ)∵函數(shù)圖象過點A(0,1)、B(年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image186.gif) ,1)
,1)
年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image188.gif) ∴b=c
∴b=c
∴年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image190.gif)
∵當(dāng)年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image192.gif)
∴年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image194.gif) ③
③
聯(lián)立②③得 年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image196.gif)
年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image198.gif)
(Ⅱ)①由年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image072.gif) 圖象上所有點向左平移
圖象上所有點向左平移年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image201.gif) 個單位得到
個單位得到年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image203.gif) 的圖象
的圖象
②由年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image203.gif) 的圖象上所有點的縱坐標(biāo)變?yōu)樵瓉淼?sub>
的圖象上所有點的縱坐標(biāo)變?yōu)樵瓉淼?sub>年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image206.gif) 倍,得到
倍,得到
年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image208.gif) 的圖象
的圖象
③由年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image208.gif) 的圖象上所有點向下平移一個單位,得到
的圖象上所有點向下平移一個單位,得到
年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image198.gif) 的圖象
的圖象
17.(1)證明:由題設(shè)年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image211.gif) ,得
,得
年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image213.gif)
又a1-1=1,
所以數(shù)列{an-n}是首項為1,且公比為4的等比數(shù)列.
(Ⅱ)解:由(Ⅰ)可知年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image215.gif) ,于是數(shù)列{ an }的通項公式為
,于是數(shù)列{ an }的通項公式為年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image217.gif)
所以數(shù)列{an}的前n項和年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image219.gif)
18.分析:求停車場面積,需建立長方形的面積函數(shù). 這里自變量的選取十分關(guān)鍵,通常有代數(shù)和三角兩種設(shè)未知數(shù)的方法,如果設(shè)長方形PQCR的一邊長為x(不妨設(shè)PR=x),則另一邊長年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image221.gif) ,
,
這樣SPQCR=PQ?PR=x?(100-年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image223.gif) ),但該函數(shù)的最值不易求得,如果將∠BAP作為自變量,用它可表示PQ、PR,再建立面積函數(shù),則問題就容易得多,于是可求解如下;
),但該函數(shù)的最值不易求得,如果將∠BAP作為自變量,用它可表示PQ、PR,再建立面積函數(shù),則問題就容易得多,于是可求解如下;
解:延長RP交AB于M,設(shè)∠PAB=年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image225.gif) ,則
,則
AM=90年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image227.gif)

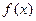
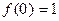
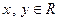
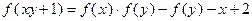 .
.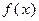 的解析式;
的解析式;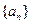 滿足:
滿足: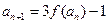 (
(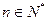 ),且
),且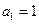 , 求數(shù)列
, 求數(shù)列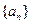 的通項;
的通項;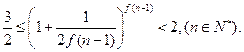
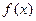
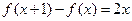
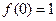
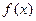 的解析式;
的解析式;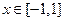 時,不等式:
時,不等式: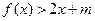 恒成立,求實數(shù)
恒成立,求實數(shù)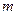 的范圍.
的范圍.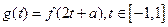
 ,求
,求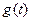 的最大值;
的最大值;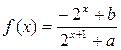
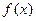 的解析式;
的解析式;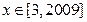 ,不等式
,不等式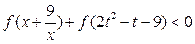 恒成立,求t
恒成立,求t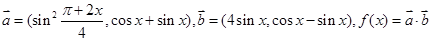
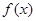 的解析式;
的解析式;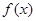 的圖象、
的圖象、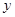 軸的正半軸及
軸的正半軸及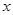 軸的正半軸三者圍成圖形的面積。
軸的正半軸三者圍成圖形的面積。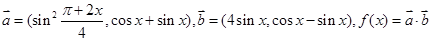
 的解析式;
的解析式; 的圖象、
的圖象、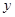 軸的正半軸及
軸的正半軸及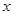 軸的正半軸三者圍成圖形的面積。
軸的正半軸三者圍成圖形的面積。年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image103.gif) 關(guān)于y軸的對稱圖形,可得
關(guān)于y軸的對稱圖形,可得年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image105.gif) 的
的年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image107.gif) 的圖象,即
的圖象,即年度高三綜合測試(二)數(shù)學(xué)試題(理科).files/image004.gif) 的圖
的圖