
�}Ŀ�б�(�����𰸺ͽ���)
�����}�M��14�֣���֪����(sh��)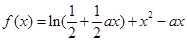 ��
��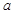 �鳣��(sh��),
�鳣��(sh��),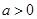 ����
����
(��)��(d��ng)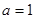 �r(sh��)����(sh��)
�r(sh��)����(sh��)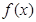 ��
��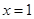 ̎���о����̣�
̎���о����̣�
(��)��(d��ng)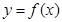 ��
��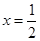 ̎ȡ�ØOֵ�r(sh��)�����P(gu��n)��
̎ȡ�ØOֵ�r(sh��)�����P(gu��n)��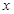 �ķ���
�ķ���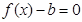 ��[0��2]��ǡ�Ѓɂ�(g��)����ȵČ�(sh��)��(sh��)������(sh��)��(sh��)
��[0��2]��ǡ�Ѓɂ�(g��)����ȵČ�(sh��)��(sh��)������(sh��)��(sh��)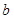 ��ȡֵ������
��ȡֵ������
(��)��(du��)�����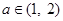 ��������
��������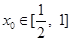 ��ʹ����ʽ
��ʹ����ʽ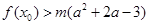 ��������(sh��)��(sh��)
��������(sh��)��(sh��)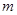 ��ȡֵ������
��ȡֵ������
�����}�M��14�֣���֪����(sh��)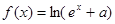 ��
��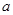 �鳣��(sh��)����
�鳣��(sh��)���� �ϵ��溯��(sh��)��
�ϵ��溯��(sh��)��
����(sh��)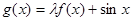 �Dž^(q��)�g
�Dž^(q��)�g
 �ϵĜp����(sh��).
�ϵĜp����(sh��).
��1����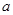 ��ֵ��
��ֵ��
��2����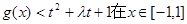 �Ϻ��������
�Ϻ�������� ��ȡֵ������
��ȡֵ������
��3��ӑՓ�P(gu��n)��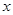 �ķ���
�ķ���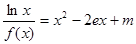 �ĸ��Ă�(g��)��(sh��).
�ĸ��Ă�(g��)��(sh��).
�����}�M��14�֣���֪����(sh��) ��
�� ����(sh��)��(sh��)
����(sh��)��(sh��) ��
�� �鳣��(sh��)����
�鳣��(sh��)����
������ ����(sh��)
����(sh��) �ĘOֵ��
�ĘOֵ��
������ ��ӑՓ����(sh��)
��ӑՓ����(sh��) �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
 ��
�� ����(sh��)��(sh��)
����(sh��)��(sh��) ��
�� �鳣��(sh��)����
�鳣��(sh��)���� ����(sh��)
����(sh��) �ĘOֵ��
�ĘOֵ�� ��ӑՓ����(sh��)
��ӑՓ����(sh��) �Ć�
�Ć� �{(di��o)�ԣ�
�{(di��o)�ԣ�.�����}�M��14�֣���֪����(sh��)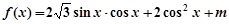 �څ^(q��)�g
�څ^(q��)�g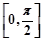 �ϵ�
�ϵ�
���ֵ��2 .
.
��1����(sh��) ��ֵ��
��ֵ��
��2���� ����
���� ,
, ,
,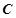 ����(du��)��߅��
����(du��)��߅��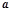 ,
,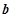 ,
,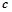 ����
����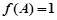 ��
��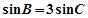 ��
��
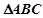 ��e��
��e��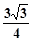 . ��߅�L(zh��ng)
. ��߅�L(zh��ng) .
.
һ���x���}
1~10 BADDA BCBCD
��������}
11��2
12��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image277.gif) 13��
13��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image279.gif) 14��8 15��45
14��8 15��45
��������}
16���⣺��?y��n)?sub>2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image164.gif) ������
������2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image281.gif) ��������������������������1�֣�
��������������������������1�֣�
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image166.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image283.gif) �����
�����2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image285.gif) ��������������������������3�֣�
��������������������������3�֣�
��?y��n)?sub>2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image172.gif) ���ʼ���
���ʼ���2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image287.gif) ��(y��ng)�֞�
��(y��ng)�֞�2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image289.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image291.gif) �ɷN��r
�ɷN��r
��1��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image289.gif) �r(sh��)��
�r(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image293.gif) ����������������������������6�֣�
����������������������������6�֣�
��2��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image291.gif) �r(sh��)��
�r(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image295.gif) ������������������������������8�֣�
������������������������������8�֣�
����2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image172.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image297.gif) ����������������������������������������9�֣�
����������������������������������������9�֣�
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image299.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image053.gif) �٣��t
�٣��t2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image302.gif) ����������������������������������������������10�֣�
����������������������������������������������10�֣�
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image299.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image053.gif) �棬�t
�棬�t2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image304.gif) ������������������������������������������������11�֣�
������������������������������������������������11�֣�
�ʌ�(sh��)��(sh��)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image011.gif) ��ȡֵ������
��ȡֵ������2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image302.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image304.gif) ��������������������������������12�֣�
��������������������������������12�֣�
17���⣺��1����12008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image179.gif) �Ľ⼯����ֻ��һ��(g��)Ԫ��֪
�Ľ⼯����ֻ��һ��(g��)Ԫ��֪
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image306.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image035.gif) ��������������������������������2�֣�
��������������������������������2�֣�
��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image309.gif) �r(sh��)������(sh��)
�r(sh��)������(sh��)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image029.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image312.gif) ���f�����˕r(sh��)���M��l��2
���f�����˕r(sh��)���M��l��2
�C�Ͽ�֪2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image314.gif) ����������������������������������3�֣�
����������������������������������3�֣�
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image316.gif) ������������������������������6�֣�
������������������������������6�֣�
��2���ɗl����֪2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image318.gif) ������������������������������7�֣�
������������������������������7�֣�
��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image320.gif) �r(sh��)����
�r(sh��)����2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image322.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image324.gif)
����2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image326.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image328.gif) ������������������������������������������������9�֣�
������������������������������������������������9�֣�
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image330.gif) �r(sh��)��Ҳ��
�r(sh��)��Ҳ��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image332.gif) ������������������������11�֣�
������������������������11�֣�
�C�ϿɵÔ�(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image189.gif) ��׃̖(h��o)��(sh��)��3������������������������������������12�֣�
��׃̖(h��o)��(sh��)��3������������������������������������12�֣�
18���⣺��1����(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image334.gif) �r(sh��)��
�r(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image336.gif) ��������������������1�֣�
��������������������1�֣�
��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image338.gif) �r(sh��)��
�r(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image340.gif) ������������������2�֣�
������������������2�֣�
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image204.gif) ��֪
��֪2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image031.gif) �������ڞ�4�ĺ���(sh��)������
�������ڞ�4�ĺ���(sh��)������
��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image342.gif) �r(sh��)
�r(sh��)
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image344.gif) ����������������������4�֣�
����������������������4�֣�
��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image346.gif) �r(sh��)
�r(sh��)
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image348.gif) ����������������������6�֣�
����������������������6�֣�
�ʮ�(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image210.gif) �r(sh��)������(sh��)
�r(sh��)������(sh��)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image072.gif) �Ľ���ʽ��
�Ľ���ʽ��
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image350.gif) ��������������������������7�֣�
��������������������������7�֣�
��2����(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image352.gif) �r(sh��)����
�r(sh��)����2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image354.gif) ����
����
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image356.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image358.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image334.gif)
�������ɂ�(g��)����ʽ�M��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image361.gif) ����������������������������������10�֣�
����������������������������������10�֣�
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image213.gif) �Ľ⼯��
�Ľ⼯��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image364.gif) ����������������12�֣�
����������������12�֣�
19���⣺��1����(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image366.gif) �r(sh��)��
�r(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image368.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image370.gif) ������������������2�֣�
������������������2�֣�
��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image372.gif) �r(sh��)��
�r(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image374.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image376.gif)
�C�ϣ���ӯ���~2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image224.gif) ���f(w��n)Ԫ���c�ծa(ch��n)��
���f(w��n)Ԫ���c�ծa(ch��n)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image135.gif) ���f(w��n)�����ĺ���(sh��)�P(gu��n)ϵ�飺
���f(w��n)�����ĺ���(sh��)�P(gu��n)ϵ�飺
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image378.gif) ����������������������������������������������4�֣�
����������������������������������������������4�֣�
��2���ɣ�1��֪����(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image366.gif) �r(sh��)��ÿ���ӯ���~��0������������������������6�֣�
�r(sh��)��ÿ���ӯ���~��0������������������������6�֣�
��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image372.gif) �r(sh��)��
�r(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image382.gif)
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image384.gif)
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image386.gif)
��(d��ng)�҃H��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image388.gif) �r(sh��)ȡ��̖(h��o)
�r(sh��)ȡ��̖(h��o)
����2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image390.gif) ��(d��ng)
��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image392.gif) �r(sh��)��
�r(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image394.gif) ���˕r(sh��)
���˕r(sh��)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image388.gif) ������������������������8�֣�
������������������������8�֣�
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image397.gif) ��(d��ng)
��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image399.gif) �r(sh��)����
�r(sh��)����2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image401.gif) ֪
֪
����(sh��)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image382.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image404.gif) ���f����
���f����2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image406.gif) ���˕r(sh��)
���˕r(sh��)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image408.gif) ������10�֣�
������10�֣�
�C�ϣ���2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image392.gif) ���t��(d��ng)�ծa(ch��n)����3�f(w��n)���r(sh��)���ɫ@���������(r��n)
���t��(d��ng)�ծa(ch��n)����3�f(w��n)���r(sh��)���ɫ@���������(r��n)
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image399.gif) ���t��(d��ng)�ծa(ch��n)����
���t��(d��ng)�ծa(ch��n)����2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image220.gif) �f(w��n)���r(sh��)���ɫ@���������(r��n)����������12�֣�
�f(w��n)���r(sh��)���ɫ@���������(r��n)����������12�֣�
20���⣺��1�����c(di��n)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image230.gif) ����
����2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image232.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image411.gif)
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image413.gif)
��?y��n)�ֱ��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image415.gif) ������
������2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image417.gif) ������������������������������3�֣�
������������������������������3�֣�
��2��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image419.gif) ��
��
��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image093.gif) ��ż��(sh��)�r(sh��)��
��ż��(sh��)�r(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image422.gif) ���攵(sh��)��
���攵(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image424.gif) ������������5�֣�
������������5�֣�
��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image093.gif) ���攵(sh��)�r(sh��)��
���攵(sh��)�r(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image422.gif) ��ż��(sh��)��
��ż��(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image426.gif) ����ȥ��
����ȥ��
�C�ϣ�����Ψһ��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image428.gif) ���ϗl������������������������������������������7�֣�
���ϗl������������������������������������������7�֣�
��3���C������ʽ2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image251.gif) ���C��
���C��
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image430.gif) �����������Ô�(sh��)�W(xu��)�w�{���C��
������������(sh��)�W(xu��)�w�{���C��
1��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image432.gif) �r(sh��)������ʽ��߅=
�r(sh��)������ʽ��߅=2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image434.gif) ��ԭ����ʽ�@Ȼ������������������������8�֣�
��ԭ����ʽ�@Ȼ������������������������8�֣�
2���O(sh��)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image436.gif)
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image438.gif) �r(sh��)��ԭ����ʽ��������
�r(sh��)��ԭ����ʽ��������2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image440.gif)
��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image442.gif) �r(sh��)
�r(sh��)
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image444.gif) =
=2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image446.gif)
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image448.gif)
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image450.gif)
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image452.gif) ����
����2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image442.gif) �r(sh��)��ԭ����ʽҲ���� ��������������11�֣�
�r(sh��)��ԭ����ʽҲ���� ��������������11�֣�
����(j��)12���ã�ԭ����ʽ��(du��)һ����Ȼ��(sh��)������ ������������������������13�֣�
21���⣺��1����2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image255.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image454.gif) ������������������1�֣�
������������������1�֣�
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image454.gif)
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image456.gif)
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image072.gif) �Ķ��x��?y��n)?sub>
�Ķ��x��?y��n)?sub>2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image458.gif) ������
������2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image460.gif)
��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image260.gif) �r(sh��)��
�r(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image463.gif)
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image465.gif)
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image467.gif)
��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image469.gif) �r(sh��)��
�r(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image471.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image072.gif) ��p����(sh��)
��p����(sh��)
��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image473.gif) �r(sh��)��
�r(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image475.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image072.gif) ��������(sh��)��������������������5�֣�
��������(sh��)��������������������5�֣�
���Ԯ�(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image260.gif) �r(sh��)��
�r(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image072.gif) �Ć��{(di��o)�f���^(q��)�g��
�Ć��{(di��o)�f���^(q��)�g��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image477.gif)
���{(di��o)�f�p�^(q��)�g��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image479.gif) ����������������6�֣�
����������������6�֣�
��2���ɣ�1��֪��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image481.gif) �r(sh��)��
�r(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image454.gif)
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image483.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image072.gif) �f���o(w��)�Oֵ��������7�֣�
�f���o(w��)�Oֵ��������7�֣�
����2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image072.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image264.gif) ̎�ИOֵ����
̎�ИOֵ����2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image260.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image486.gif)
��?y��n)?sub>2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image266.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image488.gif) ������
������2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image072.gif) ��
��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image270.gif) �φ��{(di��o)
�φ��{(di��o)
��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image270.gif) �����^(q��)�g�r(sh��)��
�����^(q��)�g�r(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image268.gif) ��������t��
��������t��
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image491.gif) ��������������������������������9�֣�
��������������������������������9�֣�
��(d��ng)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image270.gif) ��p�^(q��)�g�r(sh��)��
��p�^(q��)�g�r(sh��)��2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image268.gif) ��������t��
��������t��
2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image493.gif) �o(w��)�� ������������������13�֣�
�o(w��)�� ������������������13�֣�
����ӑՓ�Ì�(sh��)��(sh��)2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image011.gif) ��ȡֵ������
��ȡֵ������2008�ø������Ɣ�(sh��)�W(xu��)�C��Ӗ(x��n)�����ˣ�.files/image495.gif) ����������������������14�֣�
����������������������14�֣�
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com