
2009年聊城市莘縣初三春季診斷性檢測(一)
數學試卷
說明:本試題滿分120分,考試時間120分鐘。
一、選擇題(每題3分,共36分)
1.下列計算正確的是
A.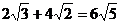 B.
B.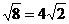
C.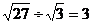 D.
D.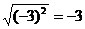
2.2008奧運會國家體育館“鳥巢”的建筑面積達25.8萬m2,用科學記數法表示應是
A.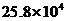 m2 B.
m2 B.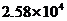 m
m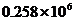 m2 D.
m2 D.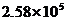 m2
m2
3.一個正方體的每個面都寫有一個漢字,其展開圖如下圖所示,則在該正方體中和“迎”相對面上所寫的漢字是
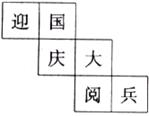
A.大 B.閱 C.兵 D.慶
4.如下圖,以O為圓心的兩個同心圓中,大圓的弦AB切小圓于點P,且AB=4,則圓環的面積(陰影)是
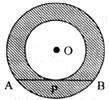
A.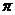 B.
B.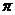 C.3
C.3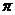 D.4
D.4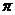
5.如下圖,將圓沿AB折疊后,圓弧恰好經過圓心,則 的度數等于
的度數等于
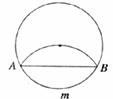
A.60° B.90° C.120° D.150°
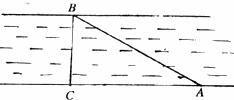
6.已知如下圖,小明為測村附近小河的寬度,在河岸上取了兩點A、C,并使AC⊥BC,若測得AC=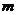 ,
,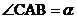 ,則河寬BC=
,則河寬BC=
A.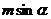 B.
B.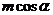 C.
C.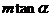 D.
D.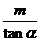
7.為貫徹兩會的教育改革精神,某縣加強了教育經費投入,2007年投入3000萬元,預計2009年投入5000萬元,設每年教育經費的平均增長率為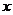 ,則列方程為
,則列方程為
A.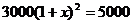 B.
B.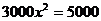
C.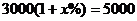 D.
D.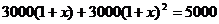
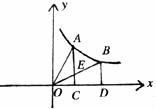
8.如下圖,過反比例函數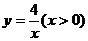 圖像上兩點A、B,分別作
圖像上兩點A、B,分別作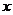 軸的垂線,垂足分別為C、D兩點,連OA、OB,設AC與OB交于點E,△AOE與梯形ECDB的面積分別為
軸的垂線,垂足分別為C、D兩點,連OA、OB,設AC與OB交于點E,△AOE與梯形ECDB的面積分別為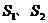 ,則
,則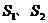 大小關系是
大小關系是
A.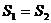 B.
B.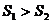
C.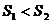 D.
D.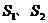 大小不確定
大小不確定
9.已知:如下圖,拋物線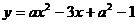 ,那么
,那么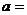
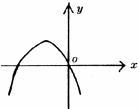
A.1 B.-1 C.±1 D.0
10.如下圖,一扇形花紙片OAB,已知OA=60cm,∠AOB=120°,小明將OA、OB合攏成一個圓錐形的生日帽(接縫忽略不計),則生日帽的底面半徑為
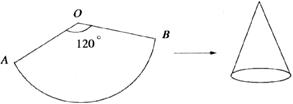
A.10cm B.20cm C.24cm D.30cm
11.小華的哥哥在西藏工作,今年“五一”她想讓哥哥帶幾本科技書回家,于是發短信告之,可一時記不清哥哥手機號碼后三位數字的順序,只記得是0、2、8三個數字,則小華一次發短信成功的概率是
A.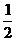 B.
B.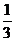 C.
C.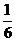 D.
D.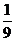
12.在密碼學中,能看到的為明碼,對明碼處理后得到的內容為密碼,有一密碼,將26個英文字母a、b、c……z(不論大小寫)依次對應1、2……26(見表格),當明碼號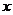 為奇數時,密碼號
為奇數時,密碼號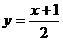 ,當明碼號
,當明碼號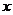 為偶數時,密碼號
為偶數時,密碼號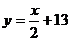
字母
a
b
c
d
e
f
g
h
i
j
k
l
m
n
o
p
q
r
s
t
u
v
w
x
y
z
序號
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
按上述規定,將明碼love譯成密碼是
A.gawq B.shxc C.sdri D.love
二、填空(3×5=15分,只要求寫出最后結果)
13.兩圓的半徑分別為3、4,圓心距為1,則兩圓的位置關系是__________。
14.對于實數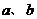 ,定義一種新運算
,定義一種新運算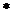 為:
為: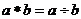 ,則
,則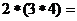 __________。
__________。
15.飛機著陸后滑行距離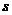 (米)與滑行時間
(米)與滑行時間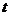 (秒)滿足:
(秒)滿足: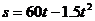 ,那么飛機著陸后滑行__________秒,才能停下來。
,那么飛機著陸后滑行__________秒,才能停下來。
16.若關于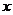 的分式方程
的分式方程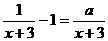 有增根,則
有增根,則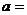 __________。
__________。
17.已知關于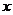 的不等式組
的不等式組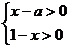 的整數解只有2個,則
的整數解只有2個,則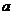 的取值范圍是__________。
的取值范圍是__________。
三、解答題(共69分,步驟要合理)
18.(6分)先化簡,再選一個你喜歡的值代入(要適合喲!)
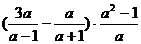
19.(8分)如下圖,E為正方形ABCD的邊AB上的動點,EF⊥DE交BC于點F。
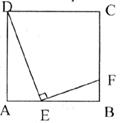
(1)求證:△ADE∽△BEF
(2)設正方形的邊長為4,AE=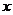 ,BF=
,BF=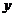 ,當
,當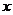 為何值時,
為何值時,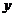 有最大值?最大值是多少?
有最大值?最大值是多少?
20.(8分)如下圖,點A、B、D、E在⊙O上,弦AE、BD的延長線交于點C,若AB是⊙O的直徑,D為BC中點。
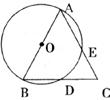
(1)試判斷AB、AC大小,并證明。
(2)在上述題設條件下,△ABC還須滿足什么條件,點E一定是AC的中點?(直接寫出結論)
21.(8分)2008北京奧運會剛剛過去,2012年倫敦奧運會已在向世人招手。某校學生會,為了了解全校同學最想收看倫敦奧運會哪種比賽項目的情況,隨機調查了200名同學,根據調查結果作了頻數分布表:
最想收看的項目
頻率(人數)
頻率
足球
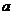
0.14
籃球
36
0.18
排球
16
0.08
羽毛球
30
0.15
乒乓球
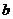
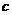
游泳
16
0.08
跳水
20
0.10
田徑
2
0.01
合計
200
(1)補全頻數分布表。
(2)根據統計結果,請寫出至少兩條正確的結論。
(3)據以上信息,作為中學生的你,對中國體育的發展有何建議?
(4)根據以上調查估計,該校5100名學生中,最想收看游泳比賽的人數是多少?
22.(8分)在一次數學課上,老師讓同學們把矩形ABCD折疊,使B、D兩點重合,折痕為直線MN,折痕與AD、BC分別交于M、N兩點。
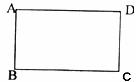
試問:(1)你能在圖上用尺規作圖畫出其折痕嗎?(保留作圖痕跡即可)
(2)若AB=1cm,AD=2cm,AM的長是多少呢。
23.(10分)甲、乙兩人騎自行車同時前往A地,他們距A地的距離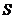 (km)與行駛時間
(km)與行駛時間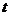 (h)之間的關系如圖。
(h)之間的關系如圖。
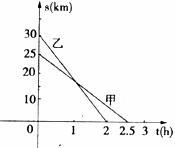
(1)甲、乙兩人的速度各是多少?
(2)寫出甲、乙兩人距A地的距離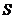 與行駛時間
與行駛時間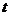 的關系式(任選一個)
的關系式(任選一個)
(3)出發多長時間甲與乙相遇?
24.(10分)如下圖,某幼兒園為了加強安全管理,決定將園內滑滑板的傾斜角由45°降為30°,已知原滑滑板AB長5米,點D、B、C在同一水平地面上。
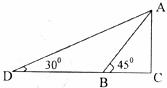
(1)改善后的滑滑板會加長多少?(保留3個有效數字)
(2)若滑滑板的正前方能有3米的空地就能保證安全,原滑滑板的前方有6米長的空地,像這樣改造是否可行?說明理由。(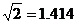 、
、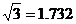 、
、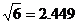 )
)
25.(11分)如下圖,在平面直角坐標系中,等腰梯形AOBC的四個頂點坐標分別為A(2,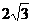 )、O(0,0)、B(8,0)、C(6,
)、O(0,0)、B(8,0)、C(6,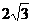 )。
)。
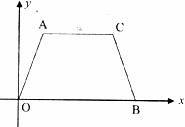
(1)求等腰梯形AOBC的面積。
(2)試說明點A在以OB為直徑的圓上。
(3)在第一象限內確定一點M,使△MOB與△AOB相似,求出所有符合條件的點M 的坐標。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com