
2008-2009學年度濰坊市高密初中學段第二學期七年級期中考試
數學試卷
時間:90分鐘 總分:120分
一、選擇題(每小題3分,共計36分)請把正確答案的序號填入下表中.
1.如果∠1+∠2+∠3=180°,那么∠1、∠2、∠3中不可能
A.有兩個鈍角,一個銳角 B.都是銳角
C.有兩個銳角,一個鈍角 D.有兩個銳角,一個直角
2.如下圖,下列說法錯誤的是
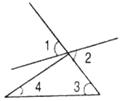
A.∠1和∠3是同位角 B.∠2和∠3是內錯角
C.∠1和∠4是內錯角 D.∠3和∠4是同旁內角
3.如下圖,AB∥CD,∠B=23°,∠D=42°,則∠E=______
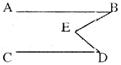
A.23° B.42° C.65° D.19°
4.如下圖,a∥b,∠1的度數是∠2的一半,則∠3等于
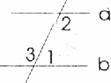
A.60° B.100° C.120° D.130°
5.如下圖,下列條件中,能判定DE∥AC的是
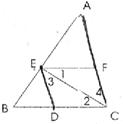
A.∠EDC=∠EFC B.∠AFE=∠ACD C.∠3=∠4 D.∠1=∠2
6.己知點A(a,b)在第二象限,則點Q(a,-b)在第( )象限
A.― B.二 C.三 D.四
7.解方程組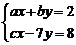 時,某同學把c看錯后得到
時,某同學把c看錯后得到 ,而正確的解是
,而正確的解是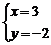 ,那么a、b、c的值是
,那么a、b、c的值是
A.a=4,b=5,c=-2 B.a,b不能確定,c=-2
C.a=4,b=7,c=2 D.a,b,c的值不能確定
8.直線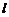 外一點P與直線
外一點P與直線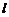 上的點Q的距離是
上的點Q的距離是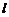 的距離
的距離
A.等于
9.如下圖,一次函數的圖像經過點A,且與正比例函數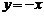 的圖像交于點B,則一次函數的表達式是
的圖像交于點B,則一次函數的表達式是
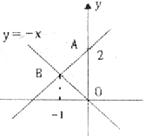
A.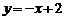 B.
B.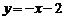 C.
C.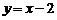 D.
D.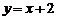
10.已知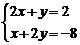 ,那么
,那么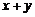 與
與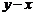 的值分別是
的值分別是
A.2,-10 B.-2,
11.如果∠1與∠2互為補角,且∠1>∠2,那么∠2的余角等于
A.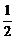 (∠1+∠2) B.
(∠1+∠2) B.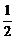 ∠1 C.
∠1 C.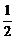 (∠1-∠2) D.∠1-∠2
(∠1-∠2) D.∠1-∠2
12.某出租車的收費標準如下圖所示,如果一乘客只有19元錢,那么他乘此出租車最遠能到達( )公里處.
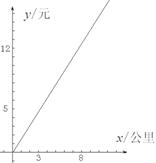
A.12 B.13 C.14 D.15
二、填空題(每題3分,共計24分)
13.甲看乙的方向是北偏西25°,那么乙看甲的方向是________.
14.己知OC是從∠AOB的頂點O引出的一條射線,若∠AOB=60°,∠AOB=2∠BOC,則∠AOC=________.
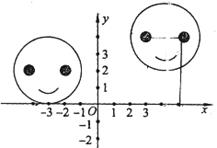
15.如下圖,在直角坐標系中,右邊的圖案是由左邊的圖案經過平移得到的。在邊圖案中左眼、右眼的坐標分別是(-4,2),(-2,2),右邊圖案中左眼的坐標是(3,4),則右邊圖案中右眼的坐標是________.
16.如下圖,AB∥CD,直線EF分別交AB、CD于點F、E,FG平分∠EFC,交AB于G.若∠1=80°,則∠FGE=________.
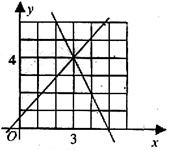
17、函數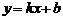 與
與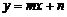 的圖象如圖所示,則方程組
的圖象如圖所示,則方程組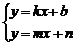 的解是________.
的解是________.
18.點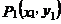 、點
、點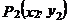 是一次函數
是一次函數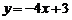 圖像上的兩點,且
圖像上的兩點,且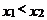 ,則
,則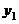 與
與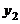 的大小關系是________.
的大小關系是________.
19.已知一次函數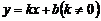 像經過點(0,1),且
像經過點(0,1),且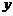 隨
隨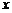 的增大而減小,請你寫出一個符合上述條件的函數關系式________.
的增大而減小,請你寫出一個符合上述條件的函數關系式________.
20.若方程組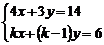 的解中
的解中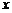 與
與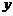 的值相等,則
的值相等,則 為________.
為________.
二、解答題(共60分)
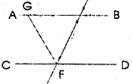
21.(4分)推理填空,如下圖,EF∥AD,∠1=∠2,∠BAC=70°.將求∠AGD的過程填寫完整:
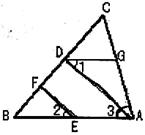
因為EF∥AD,所以∠2=________.
又因為∠1=∠2,所以∠1=∠3.
所以AB∥________.
所以∠BAC+________=180°.
又因為∠BAC=70°,所以∠AGD=________.
22.(8分)如下圖,直線AB,CD相交于點O,∠DOE=∠BOD,OF平分∠AOE,如果∠AOC=28°,那么∠EOF是多少度?
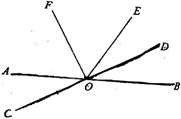
23.(8分)解方程組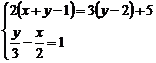
24.(10分)已知一次函數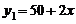 與
與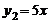 ,回答下列問題:
,回答下列問題:
(1)能否說函數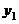 的值比函數
的值比函數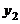 的值大?為什么?
的值大?為什么?
(2)這兩個函數是否都隨著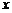 的增大而增大?當
的增大而增大?當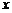 增加1個單位時,這兩個函數的值分別增加多少?
增加1個單位時,這兩個函數的值分別增加多少?
(3)當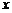 從1開始逐漸增大時,哪個函數的值先超過100?
從1開始逐漸增大時,哪個函數的值先超過100?
25.(10分)已知一次函數的圖像交正比例函數圖像于M點,交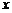 軸于點N(-6,0),又知點M位于第二象限,其橫坐標為-4,若△MON面積為15,求正比例函數和一次函數的解析式。
軸于點N(-6,0),又知點M位于第二象限,其橫坐標為-4,若△MON面積為15,求正比例函數和一次函數的解析式。
26.(10分)(任選一題,若兩題都選按得分最少的題記分,本題最高10分)
(1)某班進行個人投籃比賽,有1人未進球,有2人各進一球,有7人各進2球,有2人各進5球,沒有人進5球以上,小英和一些同學各進3球,小亮和一些同學各進4球。已知進球3個或3個以上的同學平均進3.5個球,進球4個或4個以下的同學平均每人進2.5個球,問進3個球和進4個球的人數各是多少?
(2)上杭教育服裝廠要生產一批某種型號的學生服裝,已知3米長的布料可做上衣2件或褲子3條,一件上衣和一條褲子為一套,計劃用600米長的這種布料生產,應分別用多少布料生產上衣和褲子才能恰好配套?共能生產多少套?
27.(10分)(任選一題,若兩題都選按得分最少的題記分,本題最高10分)
(1)甲乙兩輛汽車在一條公路上勻速行駛,為了確定汽車的位置,我們用數軸O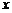 表示這條公路,原點O為零千米路標(如圖1),并作如下約定:
表示這條公路,原點O為零千米路標(如圖1),并作如下約定:
①速度v>0,表示汽車向數軸正方向行駛;速度v<0,表示汽車向數軸負方向行駛;速度v=0,表示汽車靜止.
②汽車位置在數軸上的坐標s>0,表示汽車位于零千米路標的右側;汽車位置在數軸上的坐標s<0,表示汽車位于零千米路標的左側;汽車位置在數軸上的坐標s=0,表示汽車恰好位于零千米路標處.
遵照上述約定,將這兩輛汽車在公路上勻速行駛的情況,以一次函數圖象的形式畫在了同一直角坐標系中,如圖2.
請解答下列問題:
①就這兩個一次函數圖像所反映的兩汽車在這條公路上行駛的狀況填寫如下的表格.
行駛方向
速度的大小(km/h)
出發前的位置
甲車
乙車
②甲乙兩車能否相遇?如能相遇,求相遇時的時刻及在公路上的位置;如不能相遇,請說明理由.

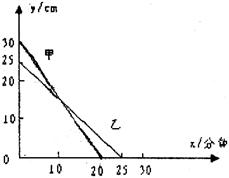
(2)在一次蠟燭燃燒實驗中,甲、乙兩根蠟燭燃燒時剩余的高度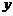 (cm)與燃燒時間
(cm)與燃燒時間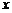 (分鐘)的關系如下圖所示,根據圖像提供的信息解答下列問題:
(分鐘)的關系如下圖所示,根據圖像提供的信息解答下列問題:
①指出兩根蠟燭燃燒前的高度;
②分別求出甲、乙兩根蠟燭燃燒時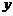 與
與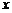 之間的函數關系式;
之間的函數關系式;
③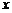 為何值時,甲、乙兩根蠟燭在燃燒過程中的高度相等.
為何值時,甲、乙兩根蠟燭在燃燒過程中的高度相等.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com