
高三數學專題講座(復數)2001年5月10日
1、(2000年)在復平面內,把復數 對應的向量按順時針方向旋轉
對應的向量按順時針方向旋轉 ,所得向量對應的復數是
,所得向量對應的復數是
(A) (B)
(B) (C)
(C) (D)
(D)
2、(2000年春季)復數 則
則 在復平面內的對應點位于
在復平面內的對應點位于
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
3、(2000年春季)設復數z1=2sin +icos
+icos
 在復平面上對應向量
在復平面上對應向量 ,將
,將 按順時針方向旋轉
按順時針方向旋轉 后得到向量
后得到向量 ,
, 對應的復數為Z2=r(cosj+isinj),則tgj=
對應的復數為Z2=r(cosj+isinj),則tgj=
(A) (B)
(B) (C)
(C) (D)
(D)
4、(2000年上海)設復數 滿足
滿足 ,且
,且 在復平面上對應的點在第二、四象限的角平分線上,
在復平面上對應的點在第二、四象限的角平分線上, ,求
,求 和
和 的值.
的值.
5、(1999年)設復數 ,求函數
,求函數 的最大值及對應的
的最大值及對應的 的值。
的值。
6、(1998年)復數?i的一個立方根是i,它的另外兩個立方根是
(A)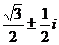 (B)
(B)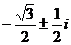 (C)
(C)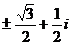 (D)
(D)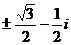
7、(1997年)已知復數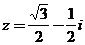 ,
,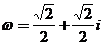 ,復數
,復數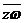 、
、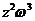 在復平面上所對應的點分別為P、Q。證明△OPQ是等腰直角三角形(其中O為原點)
在復平面上所對應的點分別為P、Q。證明△OPQ是等腰直角三角形(其中O為原點)
8、(1996年)復數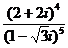 等于
等于
(A)、1+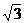 i (B)、-1+
i (B)、-1+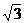 i (C)、1-
i (C)、1-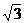 i (D)-1-
i (D)-1-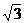 i
i
9、(1995年)在復平面上,一個正方形的四個頂點按照逆時針方向依次為Z1, Z2 ,Z3
,O(其中O是原點),已知Z2對應復數Z2=1+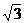 i。求Z1和Z2對應的復數。
i。求Z1和Z2對應的復數。
10、(1994年)如果復數z滿足 |z+ i |+ | z-i |=2,那么 | z+i+1 |的最小值是
(A)1 (B)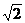 (C)2 (D)
(C)2 (D)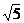
11、(1994年)已知z=1+i,(1)設w=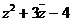 ,求w的三角形式;
,求w的三角形式;
(2)如果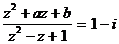 ,求實數a、b的值。
,求實數a、b的值。
12、(1993年)設復數z=cosq+isinq (0<q<p),w=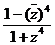 ,并且|w|=
,并且|w|=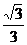 ,argw<
,argw<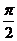 , 求 q
, 求 q
13、(2001年春季)已知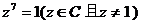 .
.
(Ⅰ)證明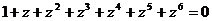 ;
;
(Ⅱ)設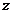 的輻角為
的輻角為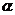 ,求
,求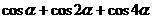 的值.
的值.
14、(2000年上海)復數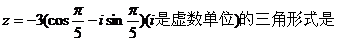
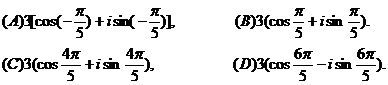
15、(2000年上海)已知復數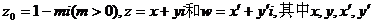 均為實數,
均為實數,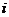 為虛數單位,且對于任意復數
為虛數單位,且對于任意復數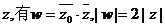 。
。
(1)試求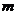 的值,并分別寫出
的值,并分別寫出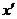 和
和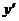 用
用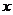 、
、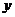 表示的關系式;
表示的關系式;
(2)將(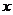 、
、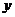 )作為點
)作為點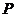 的坐標,(
的坐標,(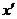 、
、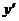 )作為點
)作為點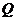 的坐標,上述關系可以看作是坐標平面上點的一個變換:它將平面上的點
的坐標,上述關系可以看作是坐標平面上點的一個變換:它將平面上的點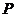 變到這一平面上的點
變到這一平面上的點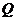 ,
,
當點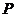 在直線
在直線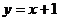 上移動時,試求點
上移動時,試求點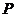 經該變換后得到的點
經該變換后得到的點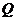 的軌跡方程;
的軌跡方程;
(3)是否存在這樣的直線:它上面的任一點經上述變換后得到的點仍在該直線上?若存在,試求出所有這些直線;若不存在,則說明理由。
1、B
2、D
3、A
4、[解法一]設
而
又∵ 在復平面上對應的點在第二、四象限的角平分線上,
在復平面上對應的點在第二、四象限的角平分線上,
∴ ,得
,得 .
.
∴ . 即
. 即 ;
; ,
,
當 時,有
時,有 ,即
,即 ,得
,得 .
.
當 時,同理可得
時,同理可得 .
.
[解法二] ,∴
,∴ ,
,
得
或
 得
得 .
.
當 時,有
時,有 ,即
,即 ,得
,得 .
.
當 時,同理可得
時,同理可得 .
.
5、解:由
由 得
得
故

當且僅當 時,即
時,即 時,上式取等號.
時,上式取等號.
所以當 時,函數
時,函數 取最大值
取最大值
6、D
7、解:因為
因為
于是
由此得OP⊥OQ,|OP|=|OQ| .
由此知△OPQ有兩邊相等且其夾角為直角,故△OPQ為等腰直角三角形。
8、B
9、解:設Z1,Z3對應的復數分別為
依題設得


10、A
11、(1)
(2)
12、 ,
, 或
或
13、解:(Ⅰ)由 

 ,
,
得 . ……4分
. ……4分
因為  ,
, ,
,
所以  . ……6分
. ……6分
(Ⅱ)因為 ,
,
所以  ,而
,而 ,所以
,所以 ,
,
 ,同理
,同理 ,
, .
.
由(Ⅰ)知  ,
,
即  ,
,
所以  的實部為
的實部為 , ……8分
, ……8分
而 的輻角為
的輻角為 時,復數
時,復數 的實部為
的實部為
 ,
,
所以  ……12分
……12分
14、C
15、[解](1)由題設, ,
,
于是由 ,
…(3分)
,
…(3分)
因此由 ,
,
得關系式 …(5分)
…(5分)
[解](2)設點 在直線
在直線 上,則其經變換后的點
上,則其經變換后的點 滿足
滿足
 ,
…(7分)
,
…(7分)
消去 ,得
,得 ,
,
故點 的軌跡方程為
的軌跡方程為 …(10分)
…(10分)
[解](3)假設存在這樣的直線,∵平行坐標軸的直線顯然不滿足條件,
∴所求直線可設為 ,
…(12分)
,
…(12分)
[解法一]∵該直線上的任一點 ,其經變換后得到的點
,其經變換后得到的點
 仍在該直線上,
仍在該直線上,
∴ ,
,
即 ,
,
當 時,方程組
時,方程組 無解,
無解,
故這樣的直線不存在。 …(16分)
當 時,由
時,由
得 ,
,
解得 或
或 ,
,
故這樣的直線存在,其方程為 或
或 ,
…(18分)
,
…(18分)
[解法二]取直線上一點 ,其經變換后的點
,其經變換后的點 仍在該直線上,
仍在該直線上,
∴ ,
,
得 ,
…(14分)
,
…(14分)
故所求直線為 ,取直線上一點
,取直線上一點 ,其經變換后得到的點
,其經變換后得到的點 仍在該直線上。
仍在該直線上。
∴ ,
…(16分)
,
…(16分)
即 ,得
,得 或
或 ,
,
故這樣的直線存在,其方程為 或
或 ,
…(18分)
,
…(18分)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com