
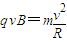 ,解得v=
,解得v= .
.
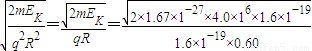 T=0.48T.
T=0.48T.

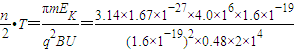 ≈1.4×10-3s.
≈1.4×10-3s. =
=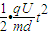
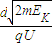 =1.4×10-9 s.
=1.4×10-9 s.

科目:高中物理 來源: 題型:
 美國物理學家勞倫斯于1932年發(fā)明的回旋加速器,應用帶電粒子在磁場中做圓周運動的特點,能使粒子在較小的空間范圍內經過電場的多次加速獲得較大的能量,使人類在獲得以較高能量帶電粒子方面前進了一步,如圖所示為一種改進后的回旋加速器示意圖,其中盒縫間的加速電場場強大小恒定,且被限制在A、C板間,帶電粒子從P0處靜止釋放,并沿電場線方向射入加速電場,經加速后再進入D形盒中的勻強磁場做勻速圓周運動,盒縫間隙很小,可以忽略不計.對于這種改進后的回旋加速器,下列說法正確的是( )
美國物理學家勞倫斯于1932年發(fā)明的回旋加速器,應用帶電粒子在磁場中做圓周運動的特點,能使粒子在較小的空間范圍內經過電場的多次加速獲得較大的能量,使人類在獲得以較高能量帶電粒子方面前進了一步,如圖所示為一種改進后的回旋加速器示意圖,其中盒縫間的加速電場場強大小恒定,且被限制在A、C板間,帶電粒子從P0處靜止釋放,并沿電場線方向射入加速電場,經加速后再進入D形盒中的勻強磁場做勻速圓周運動,盒縫間隙很小,可以忽略不計.對于這種改進后的回旋加速器,下列說法正確的是( )查看答案和解析>>
科目:高中物理 來源: 題型:閱讀理解
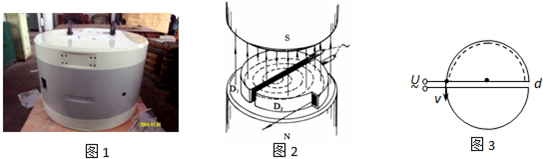
查看答案和解析>>
科目:高中物理 來源: 題型:
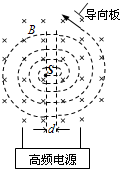 正電子發(fā)射計算機斷層(PET)是分子水平上的人體功能顯像的國際領先技術,它為臨床診斷和治療提供全新的手段.
正電子發(fā)射計算機斷層(PET)是分子水平上的人體功能顯像的國際領先技術,它為臨床診斷和治療提供全新的手段.查看答案和解析>>
科目:高中物理 來源: 題型:

查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com