
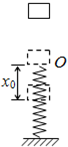
 如圖所示,一根輕彈簧豎直直立在水平面上,下端固定.在彈簧正上方有一個物塊從高處自由下落到彈簧上端O,將彈簧壓縮.當彈簧被壓縮了x0時,物塊的速度減小到零.從物塊和彈簧接觸開始到物塊速度減小到零過程中,物塊的加速度大小a隨下降位移大小x變化的圖象,可能是圖中的
如圖所示,一根輕彈簧豎直直立在水平面上,下端固定.在彈簧正上方有一個物塊從高處自由下落到彈簧上端O,將彈簧壓縮.當彈簧被壓縮了x0時,物塊的速度減小到零.從物塊和彈簧接觸開始到物塊速度減小到零過程中,物塊的加速度大小a隨下降位移大小x變化的圖象,可能是圖中的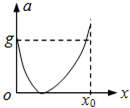


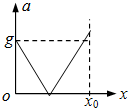
 ,a與x是線性關系,當x增大時,a減小;
,a與x是線性關系,當x增大時,a減小; -g,a與x是純性關系,當x增大時,a增大.
-g,a與x是純性關系,當x增大時,a增大.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中物理 來源: 題型:
 如圖所示,一根輕彈簧豎直放在水平地面上,一個物塊從高處自由下落到彈簧上端O,將彈簧壓縮,彈簧被壓縮x0時物塊的速度變為零.從物塊與彈簧接觸開始,物塊的速度v的大小隨下降的位移x變化情況與下列四個圖象中的哪一個比較一致?( )
如圖所示,一根輕彈簧豎直放在水平地面上,一個物塊從高處自由下落到彈簧上端O,將彈簧壓縮,彈簧被壓縮x0時物塊的速度變為零.從物塊與彈簧接觸開始,物塊的速度v的大小隨下降的位移x變化情況與下列四個圖象中的哪一個比較一致?( )查看答案和解析>>
科目:高中物理 來源: 題型:
 如圖所示,一根輕彈簧在不掛重物時,指針正對刻度5,當掛上80N的重物時,指針正對刻度45,若指針正對刻度35,則所掛重物的重力為(設彈簧的形變始終未超過彈性限度)( )
如圖所示,一根輕彈簧在不掛重物時,指針正對刻度5,當掛上80N的重物時,指針正對刻度45,若指針正對刻度35,則所掛重物的重力為(設彈簧的形變始終未超過彈性限度)( )查看答案和解析>>
科目:高中物理 來源: 題型:
 如圖所示,一根輕彈簧豎立在地面上,其下端和地面固定連接,另外一個小球P從彈簧的正上方、距離彈簧一定高度自由下落,不計空氣阻力和碰撞熱能損失,則( )
如圖所示,一根輕彈簧豎立在地面上,其下端和地面固定連接,另外一個小球P從彈簧的正上方、距離彈簧一定高度自由下落,不計空氣阻力和碰撞熱能損失,則( )查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com