
(12分)如圖所示,在xoy第一象限內分布有垂直xoy向外的勻強磁場,磁感應強度大小B=2.5×10-2T。在第二象限緊貼y軸和x軸放置一對平行金屬板MN(中心軸線過y軸),極板間距d=0.4m;極板與左側電路相連接,通過移動滑動頭P可以改變極板MN間的電壓。a、b為滑動變阻器的最下端和最上端(滑動變阻器的阻值分布均勻),a、b兩端所加電壓 。在MN中心軸線上距y軸距離為L=0.4m處,有一粒子源S沿x軸正方向連續射出比荷為
。在MN中心軸線上距y軸距離為L=0.4m處,有一粒子源S沿x軸正方向連續射出比荷為 ,速度為v0=2.0×104m/s帶正電的粒子,粒子經過y軸進入磁場,經過磁場偏轉后從x軸射出磁場(忽略粒子的重力和粒子之間的相互作用)。
,速度為v0=2.0×104m/s帶正電的粒子,粒子經過y軸進入磁場,經過磁場偏轉后從x軸射出磁場(忽略粒子的重力和粒子之間的相互作用)。

(1)、當滑動頭P在a端時,求粒子在磁場中做圓周運動的半徑R0;
(2)、當滑動頭P在ab正中間時,求粒子射入磁場時速度的大小;
(3)、滑動頭P的位置不同則粒子在磁場中運動的時間也不同,求粒子在磁場中運動的最長時間。
(1) (2)
(2) (3)
(3)
【解析】
試題分析:(1)當滑動頭P在a端時,粒子在磁場中運動的速度大小為 ,根據圓周運動:
,根據圓周運動:
 解得:
解得:
(2)當滑動頭P在ab正中間時,極板間電壓 ,粒子在電場中做類平拋運動,設粒子射入磁場時沿y軸方向的分速度為
,粒子在電場中做類平拋運動,設粒子射入磁場時沿y軸方向的分速度為 :
: 



粒子射入磁場時速度的大小設為 ,
, -
-
解得: (或
(或 )
)
(注:可以證明當極板間電壓最大時,粒子也能從極板間射出)
(3)設粒子射出極板時速度的大小為 ,偏向角為α,在 磁場中圓周運動半徑為
,偏向角為α,在 磁場中圓周運動半徑為 。根據速度平行四邊形可得:
。根據速度平行四邊形可得: 又:
又: 可得:
可得:
粒子在磁場中做圓周運動的軌跡如圖,圓心為 ,與x軸交點為D,設
,與x軸交點為D,設  ,
,

根據幾何關系:
 又:
又:
可解得:
粒子在磁場中運動的周期為T:
則粒子在磁場中運動的時間:
由此可知當粒子射入磁場時速度偏轉角越大則粒子在磁場中運動的時間就越大,假設極板間電壓為最大值U時粒子能射出電場,則此粒子在磁場中運動的時間最長。
由(2)問規律可知當滑動頭P在b端時,粒子射入磁場時沿y方向的分速度: =
=
y方向偏距: ,說明粒子可以射出極板。此時粒子速度偏轉角最大,設為
,說明粒子可以射出極板。此時粒子速度偏轉角最大,設為 :
: -
故粒子在磁場中運動的最長時間:
-
故粒子在磁場中運動的最長時間:
代入數值得: (或
(或 )
)
注:當電壓最大為U時粒子能從極板間射出需要說明,若沒有說明(或證明)扣1分;沒有證明粒子射出電場的速度偏轉角越大時,粒子在磁場中運動的時間就越長,不扣
考點:本題考查了帶電粒子在電磁場中的運動
點評:帶電粒子在磁場中運動的題目解題步驟為:定圓心、畫軌跡、求半徑.


科目:高中物理 來源: 題型:
 如圖所示,在xOy坐標系的第Ⅰ象限內存在垂直紙面向外的勻強磁場,磁感應強度為B,在x>0軸上有一平面熒光屏,在y軸上距坐標原點O為L的S處有一粒子源,在某時刻同時發射大量質量為m、電荷量為q的帶正電粒子,它們的速度大小相同,速度方向均在xy平面內,與y軸正方向的夾角分布在0~180°范圍內.觀察發現:熒光屏OP之間發光,P點右側任何位置均不發光,在P、Q之間的任一位置會先后二次發光;O、Q之間的任一位置只有一次發光,測出O、P間距為
如圖所示,在xOy坐標系的第Ⅰ象限內存在垂直紙面向外的勻強磁場,磁感應強度為B,在x>0軸上有一平面熒光屏,在y軸上距坐標原點O為L的S處有一粒子源,在某時刻同時發射大量質量為m、電荷量為q的帶正電粒子,它們的速度大小相同,速度方向均在xy平面內,與y軸正方向的夾角分布在0~180°范圍內.觀察發現:熒光屏OP之間發光,P點右側任何位置均不發光,在P、Q之間的任一位置會先后二次發光;O、Q之間的任一位置只有一次發光,測出O、P間距為| 3 |
查看答案和解析>>
科目:高中物理 來源: 題型:
 如圖所示,在xOy坐標系中,將一負檢驗電荷q由y軸上a點移動到x軸上b點時,需克服電場力做功W1,若從a點移到x軸上c點時,需克服電場力做功W2,已知W1>W2.那么關于此空間存在的靜電場可能是( )
如圖所示,在xOy坐標系中,將一負檢驗電荷q由y軸上a點移動到x軸上b點時,需克服電場力做功W1,若從a點移到x軸上c點時,需克服電場力做功W2,已知W1>W2.那么關于此空間存在的靜電場可能是( )查看答案和解析>>
科目:高中物理 來源: 題型:
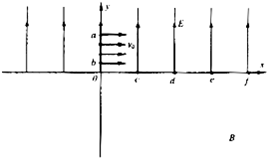 (2011?溫州二模)如圖所示,在xoy坐標系中,y>0的范圍內存在著沿y軸正方向的勻強電場,在y<0的范圍內存在著垂直紙面的勻強磁場(方向未畫出).已知oa=oc=cd=de=ef=L,ob=L/4.現有一群帶電粒子,質量為m,電荷量大小為q (重力不計),分布在y軸的a、b之間.t=0時刻,這群帶電粒子以相同的初速度v0沿x正 方向開始運動.觀察到從a點出發的帶電粒子恰好從d點第一次進入磁場,然后從O點第-次離開磁場.
(2011?溫州二模)如圖所示,在xoy坐標系中,y>0的范圍內存在著沿y軸正方向的勻強電場,在y<0的范圍內存在著垂直紙面的勻強磁場(方向未畫出).已知oa=oc=cd=de=ef=L,ob=L/4.現有一群帶電粒子,質量為m,電荷量大小為q (重力不計),分布在y軸的a、b之間.t=0時刻,這群帶電粒子以相同的初速度v0沿x正 方向開始運動.觀察到從a點出發的帶電粒子恰好從d點第一次進入磁場,然后從O點第-次離開磁場.查看答案和解析>>
科目:高中物理 來源: 題型:
 如圖所示,在xOy平面內y>0的區域中存在垂直紙面向外的勻強磁場,磁感應強度大小為B0,在y<0的區域也存在垂直紙面向外的勻強磁場(圖中未畫出),一帶正電的粒子從y軸上的P點垂直磁場入射,速度方向與y軸正向成45°.粒子第一次進入y<0的區域時速度方向與x軸正向成135°,再次在y>0的區域運動時軌跡恰與y軸相切.已知OP的距離為
如圖所示,在xOy平面內y>0的區域中存在垂直紙面向外的勻強磁場,磁感應強度大小為B0,在y<0的區域也存在垂直紙面向外的勻強磁場(圖中未畫出),一帶正電的粒子從y軸上的P點垂直磁場入射,速度方向與y軸正向成45°.粒子第一次進入y<0的區域時速度方向與x軸正向成135°,再次在y>0的區域運動時軌跡恰與y軸相切.已知OP的距離為| 2 |
查看答案和解析>>
科目:高中物理 來源: 題型:
 如圖所示,在xOy平面內,直線MN和y軸之間存在沿y軸負方向的勻強電場,在第Ⅳ象限和第I象限的射線0C右下區域存在垂直紙面向內的勻強磁場,磁感應強度大小為B.有一質量為m,帶電量為+q的質點從電場左邊界上的A點沿x軸正方向射入電場,A點與原點O的距離為d,質點到達y軸上P點時,速度方向與y軸負方向的夾角為θ=30°,P點與原點O的距離為h.接著,質點進入磁場,從磁場邊界OC上的Q點(未畫出)離開磁場之后,又從y軸上的D點垂直于y軸進入電場,最后剛好回到A點.不計質點的重力,求:
如圖所示,在xOy平面內,直線MN和y軸之間存在沿y軸負方向的勻強電場,在第Ⅳ象限和第I象限的射線0C右下區域存在垂直紙面向內的勻強磁場,磁感應強度大小為B.有一質量為m,帶電量為+q的質點從電場左邊界上的A點沿x軸正方向射入電場,A點與原點O的距離為d,質點到達y軸上P點時,速度方向與y軸負方向的夾角為θ=30°,P點與原點O的距離為h.接著,質點進入磁場,從磁場邊界OC上的Q點(未畫出)離開磁場之后,又從y軸上的D點垂直于y軸進入電場,最后剛好回到A點.不計質點的重力,求:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com