某一長直的賽道上有一輛賽車,其前方△x=200m處有一安全車正以v0=10m/s的速度勻速前進,這時賽車從靜止出發以a=2m/s2的加速度追趕.試求:
(1)賽車出發3s末的瞬時速度大小?
(2)賽車經過多長時間追上安全車?
(3)賽車追上安全車之前,從開始運動起經過多長時間與安全車相距最遠?
(4)賽車追上安全車之前與安全車最遠相距是多少米?
(5)當賽車剛追上安全車時,賽車手立即剎車,使賽車以4m/s2的加速度做勻減速直線運動,問兩車再經過多長時間第二次相遇?(設賽車可以從安全車旁經過而不發生碰撞)
解:(1)由v
t=v
0+at,賽車出發3s末的瞬時速度大小:
v
3=at
∴v
3=6m/s
故3s末的瞬時速度大小為6m/s.
(2)設賽車經過時間t追上安全車,則有:

∴t=20s
故經過20s賽車追上安全車.
(3)當兩車速度相等時相距最遠,對賽車:
v
0=at′
∴t′=5s
故經過5s兩車相距最遠.
(4)當兩車相距最遠時,
賽車位移:
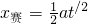
安全車位移:x
安=v
0t′
兩車之間距離△x′=x
安+△x-x
賽
∴△x′=225m
故兩車相距的最遠距離為225m.
(5)第一次相遇時賽車的速度v
20=at
20=40m/s
設從第一次相遇起再經過時間T兩車再次相遇,則:
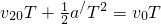
∴T=30s
但賽車速度從40m/s減為零只需10s,
所以兩車再次相遇的時間:
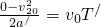
∴T′=20s
故經過20s兩車再次相遇.
分析:(1)根據勻變速直線運動的速度時間公式v=v
0+at求出賽車出發后的速度.
(2)抓住位移相等,根據運動學公式求出追及的時間.
(3)(4)在速度相等前,安全車的速度大于賽車的速度,兩車距離越來越大,速度相等后,安全車的速度小于賽車的速度,兩車的距離越來越小,則兩車速度相等時,距離最大.根據勻變速直線運動的速度時間公式求出相距最遠的時間,從而根據運動學公式得出最遠距離.
(5)根據位移相等求出第二次相遇的時間,注意要求出賽車剎車到停止的時間,因為賽車速度為零后不再運動,從而可以判斷出安全車是在賽車停止前追上還是在停止后追上.
點評:解決本題的關鍵抓住兩車位移的關系去求追及的時間.以及知道在第一次相遇前,何時兩車距離最大.


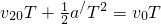
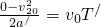


 單元全能練考卷系列答案
單元全能練考卷系列答案 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案