
 a1t2
a1t2 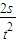 =
=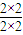 m/s2=1 m/s2
m/s2=1 m/s2 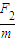 =2 m/s2
=2 m/s2  a1t2=(-2-2×2+
a1t2=(-2-2×2+ ×1×22)m=-4 m
×1×22)m=-4 m  a2t2=-
a2t2=- ×2×22 m=-4 m
×2×22 m=-4 m 

科目:高中物理 來源: 題型:
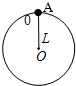 長度為L=0.4m的輕質細桿OA,A端連有一質量為m=2kg的小球,如圖所示,小球以O點為圓心在豎直平面內做圓周運動,通過最高點時小球的速率是1m/s,則此時細桿對小球的作用力為( )
長度為L=0.4m的輕質細桿OA,A端連有一質量為m=2kg的小球,如圖所示,小球以O點為圓心在豎直平面內做圓周運動,通過最高點時小球的速率是1m/s,則此時細桿對小球的作用力為( )查看答案和解析>>
科目:高中物理 來源: 題型:
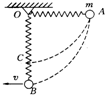 如圖所示,質量為m=2kg的小球系在輕質彈簧的一端,另一端固定在懸點O處,將彈簧拉至水平位置A處,且彈簧處于自然狀態,彈簧的原長0A=0.3m;然后小球由靜止釋放,小球到達距O點下方h=0.5m處的B點時速度為VB=2m/s,求
如圖所示,質量為m=2kg的小球系在輕質彈簧的一端,另一端固定在懸點O處,將彈簧拉至水平位置A處,且彈簧處于自然狀態,彈簧的原長0A=0.3m;然后小球由靜止釋放,小球到達距O點下方h=0.5m處的B點時速度為VB=2m/s,求查看答案和解析>>
科目:高中物理 來源: 題型:
 處于靜止狀態.兩車之間有一感應機關,在它的作用下,當滑塊滑過兩車連接處時,兩車將自動分離.現剪斷細線,滑塊先后在甲、乙小車上滑行,最終滑塊恰好滑到乙車的另一端而未滑出乙車.取g=10m/s2,求:
處于靜止狀態.兩車之間有一感應機關,在它的作用下,當滑塊滑過兩車連接處時,兩車將自動分離.現剪斷細線,滑塊先后在甲、乙小車上滑行,最終滑塊恰好滑到乙車的另一端而未滑出乙車.取g=10m/s2,求:查看答案和解析>>
科目:高中物理 來源: 題型:
 如圖所示,一輛質量為M=6kg的小車靜止在光滑的水平面上,另一質量為m=2kg的物塊(可視為質點)靜止在小車上的A點;在物塊和小車右側的擋板之間夾有一被壓縮的輕質彈簧(彈簧和物塊不相連),彈簧的彈性勢能為4J,物塊和擋板之間用細線連結.已知物塊和小車之間的動摩擦因數μ=0.2.某時刻將細線燒斷,彈簧將物塊彈開,最后物塊停在小車上的B點,取g=10m/s2.
如圖所示,一輛質量為M=6kg的小車靜止在光滑的水平面上,另一質量為m=2kg的物塊(可視為質點)靜止在小車上的A點;在物塊和小車右側的擋板之間夾有一被壓縮的輕質彈簧(彈簧和物塊不相連),彈簧的彈性勢能為4J,物塊和擋板之間用細線連結.已知物塊和小車之間的動摩擦因數μ=0.2.某時刻將細線燒斷,彈簧將物塊彈開,最后物塊停在小車上的B點,取g=10m/s2.查看答案和解析>>
科目:高中物理 來源: 題型:
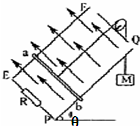 如圖所示,無限長金屬導軌EF、PQ固定在傾角為θ=30°的光滑絕緣斜面上,軌道間距L=1m,底部接入一阻值為R=0.4Ω的定值電阻,上端開口.垂直斜面向上的勻強磁場的磁感應強度B=2T.一質量為m=0.8kg的金屬棒ab與導軌接觸良好,ab與導軌間沒有摩擦,ab連入導軌間的電阻r=0.1Ω,電路中其余電阻不計.現用一質量為M=2kg的物體通過一不可伸長的輕質細繩繞過光滑的定滑輪與ab相連.由靜止釋放M,不計空氣阻力,當M下落高度h=2.0m時,ab開始勻速運動(運動中ab始終垂直導軌,并接觸良好,g=10m/s2).求:
如圖所示,無限長金屬導軌EF、PQ固定在傾角為θ=30°的光滑絕緣斜面上,軌道間距L=1m,底部接入一阻值為R=0.4Ω的定值電阻,上端開口.垂直斜面向上的勻強磁場的磁感應強度B=2T.一質量為m=0.8kg的金屬棒ab與導軌接觸良好,ab與導軌間沒有摩擦,ab連入導軌間的電阻r=0.1Ω,電路中其余電阻不計.現用一質量為M=2kg的物體通過一不可伸長的輕質細繩繞過光滑的定滑輪與ab相連.由靜止釋放M,不計空氣阻力,當M下落高度h=2.0m時,ab開始勻速運動(運動中ab始終垂直導軌,并接觸良好,g=10m/s2).求:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com