
分析 對整個過程,運用動能定理列式,可求得發動機牽引力做的功.對于從中點到斜面頂部的過程,運用動能定理列式,可求得開到中點時汽車的速度.
解答 解:對整個過程,由動能定理得:W-μmgcosθ•S-mgSsinθ=0-0
解得,發動機牽引力做的功 W=μmgScosθ+mgSsinθ
從中點到斜面頂部的過程,運用動能定理得
-μmgcosθ•$\frac{1}{2}$S-mg•$\frac{1}{2}$Ssinθ=0-$\frac{1}{2}m{v}^{2}$
可得,開到中點時汽車的速度 v=$\sqrt{gS(sinθ+μcosθ)}$
答:發動機牽引力做的功為μmgScosθ+mgSsinθ.開到中點時汽車的速度是$\sqrt{gS(sinθ+μcosθ)}$.
點評 對于涉及力在空間的效果時,運用動能定理研究,要靈活選取研究的過程,采用分段法和整體法列式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中物理 來源: 題型:計算題
 如圖甲的電路中R1=R2=100Ω是阻值不隨溫度而變的定值電阻.白熾燈泡L的伏安特性曲線如圖乙的I-U圖線所示.電源電動勢E=100V,內阻不計.求:當開關S斷開時,燈泡兩端的電壓和通過燈泡的電流以及燈泡的實際電功率;(寫出I、U、R1三者的關系式,再通過畫圖得出答案)
如圖甲的電路中R1=R2=100Ω是阻值不隨溫度而變的定值電阻.白熾燈泡L的伏安特性曲線如圖乙的I-U圖線所示.電源電動勢E=100V,內阻不計.求:當開關S斷開時,燈泡兩端的電壓和通過燈泡的電流以及燈泡的實際電功率;(寫出I、U、R1三者的關系式,再通過畫圖得出答案)查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | 電壓U加倍時,自由電子定向移動的平均速率加倍 | |
| B. | 導線長度L加倍時,自由電子定向移動的平均速率減為原來的一半 | |
| C. | 導線截面直徑d加倍時,自由電子定向移動的平均速率不變 | |
| D. | 導線截面直徑d加倍時,自由電子定向移動的平均速率加倍 |
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
| A. | 在不需要考慮物體本身的大小和形狀時,用質點來代替物體的方法叫假設法 | |
| B. | 根據速度定義式v=$\frac{△x}{△t}$,當△t非常非常小時,$\frac{△x}{△t}$就可以表示物體在t時刻的瞬時速度,該定義應用了極限思維法 | |
| C. | 玻璃瓶內裝滿水,用穿有透明細管的橡皮泥封口.手捏玻璃瓶,細管內液面高度變化,說明玻璃瓶發生形變,該實驗采用放大的思想 | |
| D. | 在推導勻變速運動位移公式時,把整個運動過程劃分成很多小段,每一小段近似看作勻速直線運動,然后把各小段的位移相加,這里采用了微元法 | |
| E. | 牛頓提出了萬有引力定律,并計算出了太陽和地球之間的引力 |
查看答案和解析>>
科目:高中物理 來源: 題型:解答題
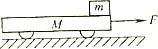 如圖所示.質量M=4kg的小車放在水平面上.在小車右端加一F=16N的水平恒力,當小車向右運動的速度達到4m/s時,在小車前端輕輕地放一個大小不計頂量為m=4kg的小物塊,物塊與小車間的動摩擦因數μ1=0.1,小車與水平面間動摩擦因數μ2=0.2,恒力F作用5s后撤去.求:
如圖所示.質量M=4kg的小車放在水平面上.在小車右端加一F=16N的水平恒力,當小車向右運動的速度達到4m/s時,在小車前端輕輕地放一個大小不計頂量為m=4kg的小物塊,物塊與小車間的動摩擦因數μ1=0.1,小車與水平面間動摩擦因數μ2=0.2,恒力F作用5s后撤去.求:查看答案和解析>>
科目:高中物理 來源: 題型:計算題
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | ${\;}_{11}^{24}$Na→${\;}_{12}^{24}$Mg+${\;}_{-1}^{0}$e是原子核衰變方程 | |
| B. | ${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{56}^{141}$Ba+${\;}_{36}^{92}$Kr+3${\;}_{0}^{1}$n是原子核人工轉變方程 | |
| C. | ${\;}_{7}^{14}$N+${\;}_{2}^{4}$He→${\;}_{8}^{17}$O+${\;}_{1}^{1}$H是原子核聚變方程 | |
| D. | ${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n是原子核裂變方程 |
查看答案和解析>>
科目:高中物理 來源: 題型:實驗題
| 砝碼質量(g) | 50 | 100 | 150 |
| 彈簧長度(cm) | 8.63 | 7.64 | 6.62 |
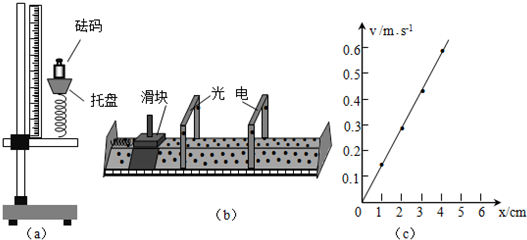
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com