
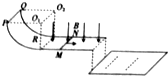
 如圖所示,電阻不計的兩光滑金屬導軌相距L固定在水平絕緣桌面上,其中半徑為R的$\frac{1}{4}$圓弧部分處在豎直平面內,水平直導軌部分處在磁感應強度為B、方向豎直向下的勻強磁場中,末端平齊.在與圓心等高的位置處有兩金屬棒MN、PQ垂直兩導軌且與導軌接觸良好.已知MN棒的質量為2m,電阻為r;PQ棒的質量為m,電阻也為r.開始時,保持PQ棒不動,將MN棒從圓弧導軌頂端無初速度釋放,當MN棒脫離導軌后,再次由靜止釋放PQ棒,最后兩棒都離開導軌落到地面上.MN、PQ兩棒落地點到導軌邊緣的水平距離之比為1:3.
如圖所示,電阻不計的兩光滑金屬導軌相距L固定在水平絕緣桌面上,其中半徑為R的$\frac{1}{4}$圓弧部分處在豎直平面內,水平直導軌部分處在磁感應強度為B、方向豎直向下的勻強磁場中,末端平齊.在與圓心等高的位置處有兩金屬棒MN、PQ垂直兩導軌且與導軌接觸良好.已知MN棒的質量為2m,電阻為r;PQ棒的質量為m,電阻也為r.開始時,保持PQ棒不動,將MN棒從圓弧導軌頂端無初速度釋放,當MN棒脫離導軌后,再次由靜止釋放PQ棒,最后兩棒都離開導軌落到地面上.MN、PQ兩棒落地點到導軌邊緣的水平距離之比為1:3.分析 (1)MN棒剛進入水平導軌時,MN棒受到的安培力最大,此時它的加速度最大.根據MN棒從圓弧導軌滑下機械能定恒求解進入磁場之前的速度大小,由E=BLv、I=$\frac{E}{2r}$、F=BIL結合求出安培力,即可由牛頓第二定律求解最大加速度.
(2)兩棒開導軌做平拋運動,根據平拋運動的規律和水平位移之比求解,根據根據動量定恒和能量定恒求解兩棒在軌道上運動過程產生的焦耳熱;
(3)根據閉合電路歐姆定律,結合電量表達式,及運動學公式,即可求解.
解答 解:(1)由題意可知,MN棒剛滑到水平導軌時,其速度達到最大.
設MN棒進入水平導軌的速度為v0,MN棒從圓弧導軌滑下機械能定恒:
2mgR=$\frac{1}{2}$×2mv02
解得:v0=$\sqrt{2gR}$
MN棒剛進入水平導軌時,設此時回路的感應電動勢為E,
E=BLv
感應電流 I=$\frac{E}{2r}$
MN棒受到的安培力為:FMN=BIL
根據牛頓第二定律,MN棒有最大加速度為
a=$\frac{{F}_{MN}}{2m}$
聯立①~⑥解得:
a=$\frac{{B}^{2}{L}^{2}\sqrt{2gR}}{4mr}$
(2)經分析可知,當MN棒離開導軌后,當PQ棒滑上水平導軌后,以v0做勻速直線運動,設MN棒離開導軌時的速度大小為v1,兩棒做平拋運動歷時均為t0,則有:
$\frac{{v}_{0}{t}_{0}}{{v}_{1}{t}_{0}}=\frac{3}{1}$,
由于MN棒和PQ棒的電阻相同,可知,MN棒在導軌上滑行的過程中,
由能量守恒定律,則有:2Q=2mgR-$\frac{1}{2}×2m{v}_{1}^{2}$
解得:Q=$\frac{8}{9}mgR$;
(3)設導軌水平部分的長度為x,MN棒在水平導軌上滑行的時間為△t,則MN棒在水平導軌滑行過程中,回路中的平均感應電流為:$\overline{I}$=$\frac{BLx}{△t(r+r)}$
又q=$\overline{I}$•△t
PQ棒在水平導軌滑行的過程中,做勻速直線運動,則有:x=v0t;
解得:t=$\frac{qr}{BLgR}\sqrt{2gR}$
答:(1)MN棒在水平直導軌上滑行的最大加速度$\frac{{B}^{2}{L}^{2}\sqrt{2gR}}{4mr}$;
(2)MN棒在導軌上滑行過程中,MN棒產生的焦耳熱$\frac{8}{9}mgR$;
(3)若MN棒在導軌上滑行的過程中通過導軌某一橫截面的電荷量為q,求PQ棒在水平直導軌上滑行的時間$\frac{qr}{BLgR}\sqrt{2gR}$.
點評 本題是電磁感應與電路、磁場、力學等知識的綜合應用,根據牛頓第二定律求加速度,以及結合運動學能夠分析出金屬棒的運動情況.考查分析和處理綜合題的能力.


科目:高中物理 來源: 題型:選擇題
| A. | 物體沿直線向某一方向運動,通過的路程等于位移的大小 | |
| B. | 物體通過一段路程,其位移不可能為零 | |
| C. | 物體沿直線某一方向運動,通過的路程就是位移 | |
| D. | 物體通過的路程不等,位移也一定不等 |
查看答案和解析>>
科目:高中物理 來源: 題型:填空題
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
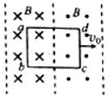 如圖所示,三條直線之間的兩個區域存在磁場,磁感應強度大小都為B,方向相反且垂直紙面.一寬為l的長方形閉合導線回路abcd,在紙面內以恒定速度v0向右運動,當運動到圖示位置時( )
如圖所示,三條直線之間的兩個區域存在磁場,磁感應強度大小都為B,方向相反且垂直紙面.一寬為l的長方形閉合導線回路abcd,在紙面內以恒定速度v0向右運動,當運動到圖示位置時( )| A. | 穿過回路磁通量的變化率為零 | |
| B. | 回路中感應電動勢大小為Blv0 | |
| C. | 回路中感應電流的方向為a→b→c→d方向 | |
| D. | 回路中ab邊與cd邊所受安培力方向相同 |
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
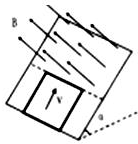 如圖所示,光滑斜面的上半部分有垂直于斜面向上的勻強磁場,邊長為L的正方體導體線框以初速度v0開始沿斜面向上進入磁場,通過一段位移x后,又沿斜面返回出發點.若x≤L,則線框在斜面上運動的過程中,下列說法正確的是( )
如圖所示,光滑斜面的上半部分有垂直于斜面向上的勻強磁場,邊長為L的正方體導體線框以初速度v0開始沿斜面向上進入磁場,通過一段位移x后,又沿斜面返回出發點.若x≤L,則線框在斜面上運動的過程中,下列說法正確的是( )| A. | 線框上滑的時間比下滑的時間短 | |
| B. | 線框的加速度先增大再減小 | |
| C. | 上滑過程中通過線框截面的電荷量比下滑過程中的大 | |
| D. | 上滑過程中產生的焦耳熱比下滑過程的多 |
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
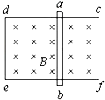 如圖所示,固定于水平面上的金屬框cdef處在豎直向下的勻強磁場中,金屬棒ab擱在框架上,與ed構成一個邊長為l的正方形,金屬棒電阻為r,其余電阻不計,開始時磁感應強度為B0,金屬棒靜止.若以t=0時起,磁感應強度均勻增加,每秒增加量為k,則( )
如圖所示,固定于水平面上的金屬框cdef處在豎直向下的勻強磁場中,金屬棒ab擱在框架上,與ed構成一個邊長為l的正方形,金屬棒電阻為r,其余電阻不計,開始時磁感應強度為B0,金屬棒靜止.若以t=0時起,磁感應強度均勻增加,每秒增加量為k,則( )| A. | 金屬棒中的感應電流的方向為b→a | |
| B. | 金屬棒中的感應電流的大小為$\frac{{k{l^{\;}}}}{r}$ | |
| C. | 金屬棒消耗的電功率為$\frac{{k}^{2}{l}^{4}}{r}$ | |
| D. | 若t=t1時金屬棒仍然靜止,金屬棒受到的最大靜摩擦力不能小于(B0+kt1)$\frac{{k{l^3}}}{r}$ |
查看答案和解析>>
科目:高中物理 來源: 題型:計算題
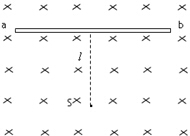 如圖所示,磁場方向垂直于紙面向里,磁感應強度B=0.60T,磁場內有一塊足夠大平行感光板ab,板面與磁場方向平行,粒子發射源S向紙面內各個方向發射v=3.0×106m/s的正粒子,S到ab的距離l=16cm.已知粒子的比荷$\frac{q}{m}$=5.0×107C/kg,求:
如圖所示,磁場方向垂直于紙面向里,磁感應強度B=0.60T,磁場內有一塊足夠大平行感光板ab,板面與磁場方向平行,粒子發射源S向紙面內各個方向發射v=3.0×106m/s的正粒子,S到ab的距離l=16cm.已知粒子的比荷$\frac{q}{m}$=5.0×107C/kg,求:查看答案和解析>>
科目:高中物理 來源: 題型:計算題
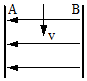 一微粒以速度v豎直向下從正中間射入水平方向的勻強電場,如圖所示.如果A、B兩板間距離為d,電勢差為U.微粒質量為m,電量為q,不計重力影響,兩金屬板足夠長.求:
一微粒以速度v豎直向下從正中間射入水平方向的勻強電場,如圖所示.如果A、B兩板間距離為d,電勢差為U.微粒質量為m,電量為q,不計重力影響,兩金屬板足夠長.求:查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
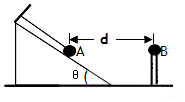 如圖所示,水平地面上固定一個光滑絕緣斜面,斜面與水平面的夾角為θ.一根輕質絕緣細線的一端固定在斜面頂端,另一端系有一個帶電小球A,細線與斜面平行.小球A的質量為m、電量為q.小球A的右側固定放置帶等量同種電荷的小球B,兩球心的高度相同、間距為d.靜電力常量為k,重力加速度為g,兩帶電小球可視為點電荷.小球A靜止在斜面上,則下列說法中正確的是( )
如圖所示,水平地面上固定一個光滑絕緣斜面,斜面與水平面的夾角為θ.一根輕質絕緣細線的一端固定在斜面頂端,另一端系有一個帶電小球A,細線與斜面平行.小球A的質量為m、電量為q.小球A的右側固定放置帶等量同種電荷的小球B,兩球心的高度相同、間距為d.靜電力常量為k,重力加速度為g,兩帶電小球可視為點電荷.小球A靜止在斜面上,則下列說法中正確的是( )| A. | 小球A與B之間庫侖力的大小為kq2/d | |
| B. | 當$\frac{q}p9vv5xb5$=$\sqrt{\frac{mgsinθ}{k}}$時,細線上的拉力為0 | |
| C. | 當$\frac{q}p9vv5xb5$=$\sqrt{\frac{mgtanθ}{k}}$時,細線上的拉力為0 | |
| D. | 當$\frac{q}p9vv5xb5$=$\sqrt{\frac{mg}{ktanθ}}$時,斜面對小球A的支持力為0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com