
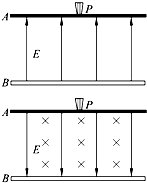
 靜電噴漆技術具有效率高、質量好、有益于健康等優點,其裝置可簡化如圖.A、B為水平放置的間距d=0.9m的兩塊足夠大的平行金屬板,兩板間有方向由B指向A的勻強電場,電場強度為E=0.1V/m.在A板的中央放置一個安全接地的靜電油漆噴槍P,油漆噴槍可向各個方向均勻地噴出初速度大小均為v0=8m/s的油漆微粒,已知油漆微粒的質量均為m=1×10-5 kg、電荷量均為q=-1×10-3 C不計空氣阻力,油漆微粒最后都能落在金屬板B上.
靜電噴漆技術具有效率高、質量好、有益于健康等優點,其裝置可簡化如圖.A、B為水平放置的間距d=0.9m的兩塊足夠大的平行金屬板,兩板間有方向由B指向A的勻強電場,電場強度為E=0.1V/m.在A板的中央放置一個安全接地的靜電油漆噴槍P,油漆噴槍可向各個方向均勻地噴出初速度大小均為v0=8m/s的油漆微粒,已知油漆微粒的質量均為m=1×10-5 kg、電荷量均為q=-1×10-3 C不計空氣阻力,油漆微粒最后都能落在金屬板B上.| 4 | 45 |
| 1 |
| 2 |
| 1 |
| 2 |
m
| ||
| R |


科目:高中物理 來源: 題型:
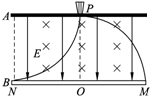
 靜電噴漆技術具有效率高、質量好、有益于健康等優點,其裝置可簡化如圖.A、B為有一定間距的兩塊平行金屬板,兩板間有方向由B指向A的勻強電場.在A板的中央放置一個安全接地的靜電油漆噴槍P,油漆噴槍可向各個方向均勻地噴出初速度大小相同且帶負電的油漆微粒,假設油漆微粒的質量、電荷量大小均相等,微粒的重力和所受空氣阻力均不計,油漆微粒最后都能落在金屬板B上.對油漆微粒,下列說法正確的是( )
靜電噴漆技術具有效率高、質量好、有益于健康等優點,其裝置可簡化如圖.A、B為有一定間距的兩塊平行金屬板,兩板間有方向由B指向A的勻強電場.在A板的中央放置一個安全接地的靜電油漆噴槍P,油漆噴槍可向各個方向均勻地噴出初速度大小相同且帶負電的油漆微粒,假設油漆微粒的質量、電荷量大小均相等,微粒的重力和所受空氣阻力均不計,油漆微粒最后都能落在金屬板B上.對油漆微粒,下列說法正確的是( )查看答案和解析>>
科目:高中物理 來源: 題型:
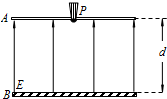 靜電噴漆技術具有效率高,浪費少,質量好,有利于工人健康等優點,其裝置示意圖如圖所示.A、B為兩塊平行金屬板,間距d=0.30m,兩板間有方向由B指向A、電場強度E=1.0×103N/C的勻強電場.在A板的中央放置一個安全接地的靜電油漆噴槍P,油漆噴槍的半圓形噴嘴可向各個方向均勻地噴出帶電油漆微粒,油漆微粒的質量m=2.0×10-15kg、電荷量為q=-2.0×10-16C,噴出的初速度v0=2.0m/s.油漆微粒最后都落在金屬板B上.微粒所受重力和空氣阻力以及微粒之間的相互作用力均可忽略.試求:
靜電噴漆技術具有效率高,浪費少,質量好,有利于工人健康等優點,其裝置示意圖如圖所示.A、B為兩塊平行金屬板,間距d=0.30m,兩板間有方向由B指向A、電場強度E=1.0×103N/C的勻強電場.在A板的中央放置一個安全接地的靜電油漆噴槍P,油漆噴槍的半圓形噴嘴可向各個方向均勻地噴出帶電油漆微粒,油漆微粒的質量m=2.0×10-15kg、電荷量為q=-2.0×10-16C,噴出的初速度v0=2.0m/s.油漆微粒最后都落在金屬板B上.微粒所受重力和空氣阻力以及微粒之間的相互作用力均可忽略.試求:查看答案和解析>>
科目:高中物理 來源: 題型:
 靜電噴漆技術具有效率高,浪費少,質量好,有利于工人健康等優點,其裝置如圖所示.A、B為兩塊平行金屬板,間距d=0.50m,兩板間有方向由B指向A,大小為E=l.0×l03N/C的勻強電場.在A板的中央放置一個安全接地的靜電油漆噴槍P.油漆噴槍的半圓形噴嘴可向各個方向均勻地噴出帶電油漆微粒,油漆微粒的初速度大小均為vo=2.0m/s,質量m=5.0×l0-16kg、帶電量為q=-2.0×10-16C.微粒的重力和所受空氣阻力均不計,油漆微粒最后都落在金屬板B上.試求:
靜電噴漆技術具有效率高,浪費少,質量好,有利于工人健康等優點,其裝置如圖所示.A、B為兩塊平行金屬板,間距d=0.50m,兩板間有方向由B指向A,大小為E=l.0×l03N/C的勻強電場.在A板的中央放置一個安全接地的靜電油漆噴槍P.油漆噴槍的半圓形噴嘴可向各個方向均勻地噴出帶電油漆微粒,油漆微粒的初速度大小均為vo=2.0m/s,質量m=5.0×l0-16kg、帶電量為q=-2.0×10-16C.微粒的重力和所受空氣阻力均不計,油漆微粒最后都落在金屬板B上.試求:查看答案和解析>>
科目:高中物理 來源: 題型:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com