
 如圖所示,已知半徑分別為R和r的甲、乙兩個光滑的圓形軌道安置在同一豎直平面內,甲軌道左側又連接一個光滑的軌道,兩圓形軌道之間由一條水平軌道CD相連,一小球自某一高度由靜止滑下,先滑過甲軌道,通過動摩擦因數為μ的CD段,又滑過乙軌道,最后離開,若小球在兩圓形軌道的最高點對軌道壓力都恰好為零,試求:
如圖所示,已知半徑分別為R和r的甲、乙兩個光滑的圓形軌道安置在同一豎直平面內,甲軌道左側又連接一個光滑的軌道,兩圓形軌道之間由一條水平軌道CD相連,一小球自某一高度由靜止滑下,先滑過甲軌道,通過動摩擦因數為μ的CD段,又滑過乙軌道,最后離開,若小球在兩圓形軌道的最高點對軌道壓力都恰好為零,試求:分析 (1)小球滾到兩圓軌道最高點均僅受重力,運用向心力公式可求出在其位置的速度.因為軌道光滑,則由機械能守恒定律可求出軌道最低點速度,從而可求出釋放小球時的高度h.
(2)由于CD段粗糙,不能運用機械守恒定律,選用動能定理,就可算出CD的長度.
解答 解:(1)小球在光滑圓軌道上滑行時,機械能守恒,設小球滑過C點時的速度為vc,通過甲環最高點速度為v′,根據小球對最高點壓力為零,有:
$mg=m\frac{{v{′^2}}}{R}$…①
取軌道最低點為零勢能點,由機械守恒定律有:
$\frac{1}{2}m{v}_{C}^{2}$=mg•2R+$\frac{1}{2}mv{′}^{2}$…②
由①、②兩式消去v′,可得:${v_c}=\sqrt{5gR}$…③
同理可得小球滑過D點時的速度為:${v_D}=\sqrt{5gr}$…④
所以小球經過C點的速度為$\sqrt{5gR}$,經過D點的速度為$\sqrt{5gr}$
小球從在甲軌道左側光滑軌道滑至C點時機械能守恒,有:$mgh=\frac{1}{2}mv_c^2$…⑤
由③、⑤兩式聯立解得:h=2.5R
因此小球釋放的高度為2.5R
(2)設CD段的長度為l,對小球滑過CD段過程應用動能定理有:
$-μmgl=\frac{1}{2}mv_D^2-\frac{1}{2}mv_c^2$…⑥
由③、④、⑥三式聯立解得:$l=\frac{{5({R-r})}}{2μ}$
則有水平CD段的長度為$\frac{{5({R-r})}}{2μ}$
答:(1)釋放小球的高度h是2.5R;
(2)水平軌道CD的長度是$\frac{5(R-r)}{2μ}$.
點評 本題中小球在軌道最高點壓力為零是解題的切入點,要明確最高點的臨界條件:重力等于向心力.在涉及力在空間的效果時,運用動能定理是常用的方法.


科目:高中物理 來源: 題型:選擇題
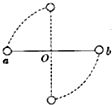
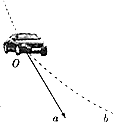 如圖,一高速行駛的汽車在一水平公路上轉彎時,如果司機不能很好地控制速度,將發生側滑而偏離正常運行路線,圖中圓弧虛線Ob代表彎道,即正常運行路線,Oa為汽車在O點時的速度方向(研究時可將汽車看作質點).下列論述正確的是( )
如圖,一高速行駛的汽車在一水平公路上轉彎時,如果司機不能很好地控制速度,將發生側滑而偏離正常運行路線,圖中圓弧虛線Ob代表彎道,即正常運行路線,Oa為汽車在O點時的速度方向(研究時可將汽車看作質點).下列論述正確的是( )| A. | 汽車轉彎時的向心力由重力提供 | |
| B. | 汽車發生側滑是因為汽車受到的合力大于所需要的向心力 | |
| C. | 若汽車在O點發生側滑,則滑動的軌跡為直線,且沿Oa方向 | |
| D. | 若汽車在O點發生側滑,則滑動的軌跡在Oa與Ob之間 |
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
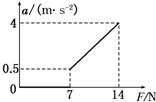 用一水平力F拉靜止在水平面上的物體,在F從0開始逐漸增大的過程中,加速度a隨外力F變化的圖象如圖所示,g=10m/s2,則可以計算出( )
用一水平力F拉靜止在水平面上的物體,在F從0開始逐漸增大的過程中,加速度a隨外力F變化的圖象如圖所示,g=10m/s2,則可以計算出( )| A. | 物體與水平面間的最大靜摩擦力 | B. | F為14N時物體的速度 | ||
| C. | a為1m/s2時物體運動的位移 | D. | 物體的質量 |
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | ①② | B. | ②④ | C. | ①④ | D. | ①③④ |
查看答案和解析>>
科目:高中物理 來源: 題型:實驗題
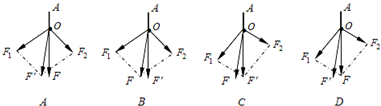
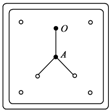 如圖所示為某同學做“驗證力的平行四邊形定則”的實驗裝置,該裝置為水平放置的木板上固定有一張白紙,一條橡皮筋的一端固定在白紙上的O點,另一端A拴兩個細繩套.
如圖所示為某同學做“驗證力的平行四邊形定則”的實驗裝置,該裝置為水平放置的木板上固定有一張白紙,一條橡皮筋的一端固定在白紙上的O點,另一端A拴兩個細繩套.查看答案和解析>>
科目:高中物理 來源: 題型:實驗題
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
 如圖所示,質量分別為m和2m的兩個小球a和b,中間用長為L的輕質桿相連,在桿的中點O處有一光滑固定轉動軸,把桿至于水平位置后釋放,在b球順時針擺動到最低位置的過程中( )
如圖所示,質量分別為m和2m的兩個小球a和b,中間用長為L的輕質桿相連,在桿的中點O處有一光滑固定轉動軸,把桿至于水平位置后釋放,在b球順時針擺動到最低位置的過程中( )| A. | b球的重力勢能減少,動能增加,b球機械能守恒 | |
| B. | a球、b球和地球組成的系統機械能守恒 | |
| C. | b球在最低點對桿的作用力為$\frac{10}{3}$mg | |
| D. | b球到達最低點時的速度為$\sqrt{gl}$ |
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
| A. | 溫度相同的物體,其分子的平均動能一定相同 | |
| B. | 在使兩個分子間的距離由很遠(r>10-9 m)減小到很難再靠近的過程中,分子間的作用力先減小后增大,分子勢能不斷增大 | |
| C. | 由于液體表面層分子間的距離大于液體內部分子間的距離,所以液體表面存在張力 | |
| D. | 根據熱力學第二定律可知:熱量能夠從高溫物體傳到低溫物體,但不可能從低溫物體傳到高溫物體 | |
| E. | 布朗運動是懸浮在液體中的固體小顆粒的運動,它間接說明了液體分子在永不停息地做無規則運動 |
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
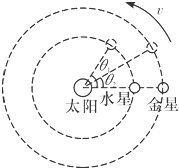 如果把水星和金星繞太陽的運動視為勻速圓周運動,從水星與金星在一條直線上開始計時,如圖所示.若天文學家測得在相同時間內水星轉過的角度為θ1;金星轉過的角度為θ2(θ1、θ2均為銳角),則由此條件可求得( )
如果把水星和金星繞太陽的運動視為勻速圓周運動,從水星與金星在一條直線上開始計時,如圖所示.若天文學家測得在相同時間內水星轉過的角度為θ1;金星轉過的角度為θ2(θ1、θ2均為銳角),則由此條件可求得( )| A. | 水星和金星繞太陽運動的周期之比 | B. | 水星和金星的密度之比 | ||
| C. | 水星和金星到太陽的距離之比 | D. | 太陽的密度 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com