
 在如圖所示的裝置中,電源電動勢為E,內阻不計,定值電阻為R1,滑動變阻器總值為R2,置于真空中的平行板電容器水平放置,極板間距為d.處在電容器中的油滴A恰好靜止不動,此時滑動變阻器的滑片P位于中點位置.
在如圖所示的裝置中,電源電動勢為E,內阻不計,定值電阻為R1,滑動變阻器總值為R2,置于真空中的平行板電容器水平放置,極板間距為d.處在電容器中的油滴A恰好靜止不動,此時滑動變阻器的滑片P位于中點位置.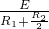
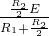 =
=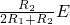 .
. =mg,所以
=mg,所以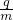 =
= .
.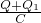
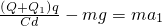
 a1t2,v1=a1t
a1t2,v1=a1t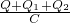
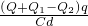 =ma2
=ma2 a2(2t)2
a2(2t)2 =
= .
.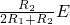 .
.  .
.

 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:高中物理 來源: 題型:
 在如圖所示的裝置中,A、B、C、D為四個平行正對的金屬板,其中B板和C板上開有小孔,分別與兩個電源相連,B和A兩板間的電壓為U,C和D兩板間電壓為2U,從靠近A板的F處釋放出一個無初速度的電子,電荷量為e.關于電子的運動,下列描述中哪些是正確的( )
在如圖所示的裝置中,A、B、C、D為四個平行正對的金屬板,其中B板和C板上開有小孔,分別與兩個電源相連,B和A兩板間的電壓為U,C和D兩板間電壓為2U,從靠近A板的F處釋放出一個無初速度的電子,電荷量為e.關于電子的運動,下列描述中哪些是正確的( )查看答案和解析>>
科目:高中物理 來源: 題型:
 (2011?廣元模擬)在如圖所示的裝置中,電源電動勢為E,內阻不計,定值電阻為R1,滑動變阻器總值為R2,置于真空中的平行板電容器水平放置,極板間距為d.處在電容器中的油滴A恰好靜止不動,此時滑動變阻器的滑片P位于中點位置.
(2011?廣元模擬)在如圖所示的裝置中,電源電動勢為E,內阻不計,定值電阻為R1,滑動變阻器總值為R2,置于真空中的平行板電容器水平放置,極板間距為d.處在電容器中的油滴A恰好靜止不動,此時滑動變阻器的滑片P位于中點位置.查看答案和解析>>
科目:高中物理 來源: 題型:
 在如圖所示的裝置中,木塊B與水平桌面的接觸是光滑的,子彈A沿水平方向射入木塊后留在木塊內.從子彈射向木塊到木塊將彈簧壓縮到最短的全過程中,下列說法正確
在如圖所示的裝置中,木塊B與水平桌面的接觸是光滑的,子彈A沿水平方向射入木塊后留在木塊內.從子彈射向木塊到木塊將彈簧壓縮到最短的全過程中,下列說法正確查看答案和解析>>
科目:高中物理 來源: 題型:閱讀理解
 (2007?蘇州二模)處在激發態的氫原子向能量較低的狀態躍遷時會發出一系列不同頻率的光,稱為氫光譜.氫光譜線的波長可以用下面的巴耳末-里德伯公式
(2007?蘇州二模)處在激發態的氫原子向能量較低的狀態躍遷時會發出一系列不同頻率的光,稱為氫光譜.氫光譜線的波長可以用下面的巴耳末-里德伯公式| 1 |
| λ |
| 1 |
| k2 |
| 1 |
| n2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com