
 如圖所示,質量為M=0.1kg、半徑為R=1.0m的質量分布均勻的圓環靜止在粗糙的水平桌面上,一質量為m=0.2kg的光滑小球以水平速度v0=6.0m/s通過環上的小孔正對環心射入環內,與環發生第一次碰撞后到第二次碰撞前小球恰好不會從小孔中穿出.假設小球與環內壁的碰撞為彈性碰撞,只考慮圓環與桌面之間的摩擦,且粗糙程度各處相同.求:
如圖所示,質量為M=0.1kg、半徑為R=1.0m的質量分布均勻的圓環靜止在粗糙的水平桌面上,一質量為m=0.2kg的光滑小球以水平速度v0=6.0m/s通過環上的小孔正對環心射入環內,與環發生第一次碰撞后到第二次碰撞前小球恰好不會從小孔中穿出.假設小球與環內壁的碰撞為彈性碰撞,只考慮圓環與桌面之間的摩擦,且粗糙程度各處相同.求:分析 ①小球與環內壁發生彈性碰撞,遵守動量守恒和機械能守恒,由動量守恒定律和機械能守恒定律結合解答.
②小球恰好不會從小孔穿出,則第一次碰撞后,環做勻減速直線運動,設經t時間與小球速度大小相等,由動量定理列式求出摩擦力.假設環在第二次碰撞前已停止,其位移由動能定理求得.根據小球的運動規律求出小球的位移,即可判斷假設是否正確.
③多次碰撞后小球和環最終靜止,系統的動能全部轉化為摩擦生熱,由此列式求解圓環通過的總位移.
解答 解:①設第一次剛碰撞完,小球和環各自的速度大小分別為v1和v2,取向左為正方向,根據動量守恒定律和機械能守恒定律,有:
mv0=mv1+Mv2
$\frac{1}{2}$mv02=$\frac{1}{2}$mv12+$\frac{1}{2}$Mv22
解得:v1=2m/s,v2=8m/s.
②第一次碰撞后經過時間t,小球恰好未從小孔中穿出,即二者共速,均為v1,由運動學規律:
$\frac{{v}_{1}+{v}_{2}}{2}t$-v1t=2R
對圓環,由動量定理:
-ft=Mv1-Mv2;
聯立解得:f=0.9N
假設環在第二次碰撞前已停止,其位移由動能定理得:
-fx2=0-$\frac{1}{2}M{v}_{2}^{2}$
解得 x2=$\frac{32}{9}$m
此時小球的位移,由運動學規律:
x1=v1•t′
設對圓環速度從v2減至0的時間為t′,由動量定理得::
-ft′=0-Mv2;
聯立得 x1=v1•$\frac{M{v}_{2}}{f}$=2×$\frac{0.1×8}{0.9}$=$\frac{16}{9}$m<$\frac{32}{9}$m
假設成立,所以在第二次碰撞前環的位移為 x2=$\frac{32}{9}$m
③多次碰撞后小球和環最終靜止,設圓滑受到的摩擦力為f,通過的總位移為x,系統的動能全部轉化為摩擦生熱:
fx=$\frac{1}{2}m{v}_{0}^{2}$
聯立解得,圓環通過的總位移為:x=4m.
答:
①第一次碰撞后圓環的速度是8.0m/s.
②第二次碰撞前圓環的位移是$\frac{32}{9}$m.
③圓環通過的總位移是4m.
點評 本題的關鍵要分析清楚物體的運動過程,應用動量守恒定律、機械能守恒定律、運動學公式、動量定理即可正確解題.涉及時間時可優先考慮動量定理.涉及位移時可優先考慮動能定理.


 新思維假期作業寒假吉林大學出版社系列答案
新思維假期作業寒假吉林大學出版社系列答案科目:高中物理 來源: 題型:填空題

查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | 應串聯一個0.1Ω的電阻 | B. | 應并聯一個0.1Ω的電阻 | ||
| C. | 應串聯一個1900Ω的電阻 | D. | 應并聯一個1900Ω的電阻 |
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | 神州十一號飛船發射過程中,航天員一直處于失重狀態 | |
| B. | 天宮二號如果受到較大的阻力作用,則軌道半徑將增大 | |
| C. | 神州十一號飛船與天宮二號在同一軌道加速后可以實現對接 | |
| D. | 神州十一號飛船與天宮二號對接后正常運行時,二者動能和引力勢能之和一定守恒 |
查看答案和解析>>
科目:高中物理 來源: 題型:計算題
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | 加速度是指物體增加的速度 | |
| B. | 加速度是描述物體速度變化的物理量 | |
| C. | 物體速度有變化則必有加速度 | |
| D. | 物體運動的速度隨加速度的增加而增加 |
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
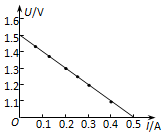 如圖是根據某次測定電池的電動勢和內阻的實驗記錄的數據作出的U-I圖象,關于這個圖象的說法中正確的是( )
如圖是根據某次測定電池的電動勢和內阻的實驗記錄的數據作出的U-I圖象,關于這個圖象的說法中正確的是( )| A. | 縱軸截距表示待測電池的電動勢,即E=1.50V | |
| B. | 橫軸截距表示短路電流,即I0=0.5A | |
| C. | 根據r=$\frac{E}{{I}_{0}}$,計算出待測電池內阻為3Ω | |
| D. | 該電池與2Ω的電阻串聯,電源的路端電壓為1V |
查看答案和解析>>
科目:高中物理 來源: 題型:實驗題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com