
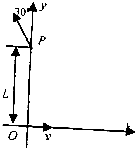
 如圖所示,在xOy平面上的某圓形區域內,存在一垂直紙面向里的勻強磁場,磁感應強大小為B.一電荷量為+q、質量為m的帶電粒子,由原點O開始沿x正方向運動,進入該磁場區域后又射出該磁場.后來,粒子經過y軸上的P點,此時速度方向與y軸的夾角為30°,已知P到O的距離為L,不計重力的影響.
如圖所示,在xOy平面上的某圓形區域內,存在一垂直紙面向里的勻強磁場,磁感應強大小為B.一電荷量為+q、質量為m的帶電粒子,由原點O開始沿x正方向運動,進入該磁場區域后又射出該磁場.后來,粒子經過y軸上的P點,此時速度方向與y軸的夾角為30°,已知P到O的距離為L,不計重力的影響.分析 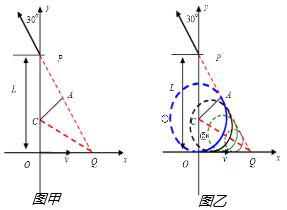 初、末速度所在直線必定與粒子的軌跡圓相切,軌跡圓圓心到兩條直線的距離(即軌道半徑)相等,因此,圓心必位于初、末速度延長線形成的角平分線QC上(如圖甲);在角平分線QC上取不同的點為圓心,由小到大作出一系列軌跡圓(如圖乙),其中以C點為圓心軌跡①是可能的軌跡圓中半徑最大的,其對應的粒子速度也最大;
初、末速度所在直線必定與粒子的軌跡圓相切,軌跡圓圓心到兩條直線的距離(即軌道半徑)相等,因此,圓心必位于初、末速度延長線形成的角平分線QC上(如圖甲);在角平分線QC上取不同的點為圓心,由小到大作出一系列軌跡圓(如圖乙),其中以C點為圓心軌跡①是可能的軌跡圓中半徑最大的,其對應的粒子速度也最大;
解答 解:(1)過P點作末速度所在直線,交x軸與Q點,經分析可知,粒子在磁場中做勻速圓周運動的軌跡的圓心必在∠OPQ的角平分線QC上,如圖甲所示,
設粒子在磁場中作勻速圓周運動的軌道半徑為r,則由牛頓第二定律有
$qvB=m\frac{{v}_{\;}^{2}}{r}$
則$r=\frac{mv}{qB}$…①
由此可知粒子速度越大,其軌道半徑越大,由圖乙可知,速度最大的粒子在磁場中運動軌跡的圓心是y軸上的C點.如圖丙所示,
速度最大時粒子的軌跡圓過O點,且與PQ相切與A點.
由幾何關系有OQ=Ltan30° ${r}_{1}^{\;}=OQtan30°$
可得${r}_{1}^{\;}=\frac{L}{3}$…②
由①②求得:$v=\frac{qBL}{3m}$
(2)將$v=\frac{qBL}{6m}$代入①式,可得${r}_{2}^{\;}=\frac{L}{6}$,粒子運動軌跡是如圖丁所示的軌跡圓②,
該軌跡圓與x軸相切于D點,與PQ相切于E點,連接DE,由幾何關系可知:
$DE=\sqrt{3}{r}_{2}^{\;}$
由于D、E點必在磁場內,故可知磁場面積最小時必定是以DE為直徑(如圖丁中③所示),即面積最小的磁場半徑為:
$R=\frac{1}{2}DE$
則磁場的最小面積為:$s=π{R}_{\;}^{2}=π(\frac{\sqrt{3}}{12}L)_{\;}^{2}=\frac{π{L}_{\;}^{2}}{48}$
答:(1)若磁場區域的大小可根據需要而改變,粒子速度的最大可能值$\frac{qBL}{3m}$;
(2)若粒子速度大小為v=$\frac{qBL}{6m}$,該圓形磁場區域的最小面積$\frac{π{L}_{\;}^{2}}{48}$
點評 本題考查了帶電粒子在磁場中的勻速圓周運動,對數學的幾何能力要求較高,關鍵畫出粒子的軌跡圖,結合牛頓第二定律以及向心力等知識進行求解.


科目:高中物理 來源: 題型:選擇題
| A. | 如不加干預,在運行一段時間后,天宮一號的動能可能會減小 | |
| B. | 如不加干預,天宮一號的軌道高度將緩慢降低 | |
| C. | 為實現對接,兩者運行速度的大小都應介于第一宇宙速度和第二宇宙速度之間 | |
| D. | 航天員在天宮一號中處于失重狀態,說明航天員不受地球引力作用 |
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
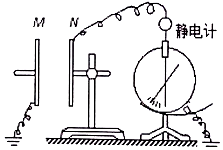 如圖所示,由M、N兩塊相互靠近的平行金屬板組成的平行板電容器,極板N與靜電計的金屬球相接,極板M與靜電計的外殼均接地.給電容器充電,靜電計指針張開一定角度.實驗過程中電容器所帶電荷量不變.下面操作能使靜電計指針張角變小的是( )
如圖所示,由M、N兩塊相互靠近的平行金屬板組成的平行板電容器,極板N與靜電計的金屬球相接,極板M與靜電計的外殼均接地.給電容器充電,靜電計指針張開一定角度.實驗過程中電容器所帶電荷量不變.下面操作能使靜電計指針張角變小的是( )| A. | 在M、N之間插入有機玻璃板 | B. | 把接地的兩根導線直接相連 | ||
| C. | 將M板向上平移 | D. | 將M板沿水平方向向左移動 |
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
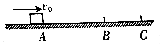 如圖所示,粗糙水平面上有A、B、C三點,AB、BC長度之比為5:3,現有一粗糙小物塊以初速度v0滑過A點后,又依次滑過B、C兩點,已知小物塊在粗糙水平面上的運動可看做勻變速直線運動,從A點運動到C點所用的時間為t,則以下說法中正確的是( )
如圖所示,粗糙水平面上有A、B、C三點,AB、BC長度之比為5:3,現有一粗糙小物塊以初速度v0滑過A點后,又依次滑過B、C兩點,已知小物塊在粗糙水平面上的運動可看做勻變速直線運動,從A點運動到C點所用的時間為t,則以下說法中正確的是( )| A. | 小物塊到達B點的速度為$\frac{2{v}_{0}}{3}$ | B. | 小物塊到達B點的速度為$\frac{{v}_{0}}{4}$ | ||
| C. | 物塊從A點運動到B點的時間為$\frac{t}{4}$ | D. | 物塊從A點運動到B點的時間為$\frac{3}{4}$t |
查看答案和解析>>
科目:高中物理 來源: 題型:計算題
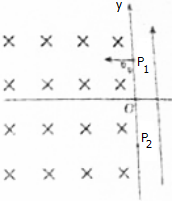 如圖所示,在x>0的空間中存在勻強電場,場強沿y軸正方向:在x<0的空間中,存在勻強磁揚,磁場方向垂直xOy平面(紙面)向里,一電量為q、質量為m的帶正電的粒子,從y軸上的P1點垂直磁場方向以速率v0進入勻強磁場中,然后從P2點進入勻強電場中,在電場中運動時經過x軸上的P3點,已知P1,P2和P3點的位置坐標分別為(0,h)、(0,-h)和(2h,0).不計帶點粒子的重力.求:
如圖所示,在x>0的空間中存在勻強電場,場強沿y軸正方向:在x<0的空間中,存在勻強磁揚,磁場方向垂直xOy平面(紙面)向里,一電量為q、質量為m的帶正電的粒子,從y軸上的P1點垂直磁場方向以速率v0進入勻強磁場中,然后從P2點進入勻強電場中,在電場中運動時經過x軸上的P3點,已知P1,P2和P3點的位置坐標分別為(0,h)、(0,-h)和(2h,0).不計帶點粒子的重力.求:查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
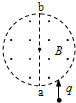 如圖,半徑為R的圓是一圓柱形勻強磁場區域的橫截面(紙面),磁感應強度大小為B,方向垂直于紙面向外.一電荷量為q(q<0)、質量為m的粒子沿平行于直徑ab的方向射入磁場區域,射入點與ab的距離為$\frac{R}{2}$.已知粒子射出磁場與射入磁場時運動方向間的夾角為60°,則粒子的速率為(不計重力)( )
如圖,半徑為R的圓是一圓柱形勻強磁場區域的橫截面(紙面),磁感應強度大小為B,方向垂直于紙面向外.一電荷量為q(q<0)、質量為m的粒子沿平行于直徑ab的方向射入磁場區域,射入點與ab的距離為$\frac{R}{2}$.已知粒子射出磁場與射入磁場時運動方向間的夾角為60°,則粒子的速率為(不計重力)( )| A. | $\frac{qBR}{2m}$ | B. | $\frac{qBR}{m}$ | C. | $\frac{3qBR}{2m}$ | D. | $\frac{2qBR}{m}$ |
查看答案和解析>>
科目:高中物理 來源: 題型:計算題
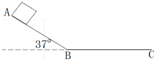 如圖所示,一固定在地面上的軌道ABC,其中AB長.S1=2m,AB與水平面間的夾角為θ=37,一小物塊自A處由靜止釋放,小物塊與軌道間的動摩擦因數均為μ=0.25,小物塊經過B點時無機械能損失(sin37°=0.6,cos37°=0.8,g取10m/s2).求:
如圖所示,一固定在地面上的軌道ABC,其中AB長.S1=2m,AB與水平面間的夾角為θ=37,一小物塊自A處由靜止釋放,小物塊與軌道間的動摩擦因數均為μ=0.25,小物塊經過B點時無機械能損失(sin37°=0.6,cos37°=0.8,g取10m/s2).求:查看答案和解析>>
科目:高中物理 來源: 題型:實驗題
 將一質量為m的小球靠近墻面豎直向上拋出,圖甲、圖乙分別是上升和下降時的頻閃照片,O點恰是運動的最高點.假設小球所受阻力大小不變,重力加速度為g,則小球向上運動的加速度大小為1.5g,受到的阻力大小為0.5mg.
將一質量為m的小球靠近墻面豎直向上拋出,圖甲、圖乙分別是上升和下降時的頻閃照片,O點恰是運動的最高點.假設小球所受阻力大小不變,重力加速度為g,則小球向上運動的加速度大小為1.5g,受到的阻力大小為0.5mg.查看答案和解析>>
科目:高中物理 來源: 題型:多選題
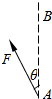 如圖所示,紙面內有一勻強電場,帶正電的小球(重力不計)在恒力F的作用下沿圖中虛線由A勻速運動至B,已知力F和AB間夾角為θ,AB間距離為d,小球帶電量為q,則下列結論正確的是( )
如圖所示,紙面內有一勻強電場,帶正電的小球(重力不計)在恒力F的作用下沿圖中虛線由A勻速運動至B,已知力F和AB間夾角為θ,AB間距離為d,小球帶電量為q,則下列結論正確的是( )| A. | 電場強度的大小為E=$\frac{Fcosθ}{q}$ | |
| B. | AB兩點的電勢差為UAB=-$\frac{Fdcosθ}{q}$ | |
| C. | 帶電小球由A運動至B過程中電勢能增加了Fdcosθ | |
| D. | 帶電小球若由B勻速運動至A,則恒力F必須反向 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com