
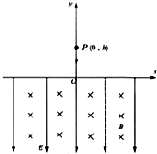
 如圖,在豎直平面內x軸下方有感應強度為B、方向垂直于紙面向里的勻強磁場和電場強度為E、豎直向下的勻強電場.一帶電小球從y軸上P(0,h)點以初速度v0豎直向下拋出.小球穿過x軸后恰好做勻速圓周運動.若不計空氣阻力,重力加速度為g.求:
如圖,在豎直平面內x軸下方有感應強度為B、方向垂直于紙面向里的勻強磁場和電場強度為E、豎直向下的勻強電場.一帶電小球從y軸上P(0,h)點以初速度v0豎直向下拋出.小球穿過x軸后恰好做勻速圓周運動.若不計空氣阻力,重力加速度為g.求:分析 (1)小球先做豎直下拋運動,根據速度位移公式列式求解進入電磁場的速度;在電磁場中做勻速圓周運動,重力和電場力平衡,洛倫茲力提供向心力,做勻速圓周運動,根據牛頓第二定律列式求解;
(2)先確定運動軌跡,然后結合圓周運動的周期公式T=$\frac{2πm}{qB}$列式求解.
解答 解:(1)在x軸上方,是勻加速直線運動,根據速度位移公式,有:
${v^2}-v_0^2=2gh$
解得:$v=\sqrt{v_0^2+2gh}$
設小球的質量為m,因帶電小球在復合場中作勻速圓周運動,故電場力一定與重力平衡,即:
mg=qE,電場力方向豎直向上,
則小球帶負電;
設在復合場中小球的運動半徑為R,則:
$qvB=m\frac{v^2}{R}$
聯立解得:R=$\frac{{E\sqrt{2gh+v_0^2}}}{Bg}$
(2)小球的運動軌跡如圖所示: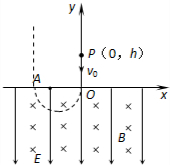
從P到O過程,有:
h=$\frac{{v}_{0}+v}{2}{t}_{1}$
從O到A過程:
${t}_{2}=\frac{T}{2}=\frac{πm}{qB}$
從A向上到返回A點過程,有:
${t}_{3}=\frac{(-v)-v}{-g}$
總時間:
t=t1+t2+t3
聯立解得:
t=$\frac{{3\sqrt{v_0^2+2gh}-{v_0}}}{g}+\frac{πE}{gB}$
答:(1)小球在x軸下方做勻速圓周運動的半徑為$\frac{{E\sqrt{2gh+v_0^2}}}{Bg}$;
(2)小球從P點出發到第三次經過x軸所用時間為$\frac{{3\sqrt{v_0^2+2gh}-{v_0}}}{g}+\frac{πE}{gB}$.
點評 本題關鍵是明確小球的受力情況和運動情況,分勻變速直線運動過程和勻速圓周運動過程進行分析,對勻速圓周運動過程,要能夠找到向心力來源,根據牛頓第二定律列式分析,不難.


科目:高中物理 來源: 題型:解答題
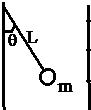 如圖所示,兩塊相距為a、足夠長的金屬板平行豎直放置,長為L的絕緣細線一端拴質量為m的帶電小球,另一端固定在左板上某點,小球靜止時絕緣線與豎直方向的夾角為θ問:
如圖所示,兩塊相距為a、足夠長的金屬板平行豎直放置,長為L的絕緣細線一端拴質量為m的帶電小球,另一端固定在左板上某點,小球靜止時絕緣線與豎直方向的夾角為θ問:查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | 冰球的加速度大于冰壺的加速度 | B. | 冰球的加速度小于冰壺的加速度 | ||
| C. | 冰球的加速度等于冰壺的加速度 |
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
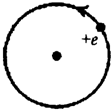
| A. | 正電子運動時不產生磁場 | |
| B. | 正電子運動時只在圓周內產生磁場 | |
| C. | 正電子運動時產生磁場,圓心處的磁場方向垂直紙面向外 | |
| D. | 正電子運動時產生磁場,圓心處的磁場方向垂直紙面向里 |
查看答案和解析>>
科目:高中物理 來源: 題型:解答題
 如圖所示,A、B兩物體的質量分別為mA=0.6kg、mB=0.4kg,放在質量為m車=1kg的足夠長的小車C上,A、B相距8cm,它們隨車以V0=1.0m/s的速度在光滑的水平地面上向右勻速運動,若在小車上加一水平向右的推力F=4N,A、B便在小車上滑動,已知A、B與小車間的動摩擦因數分別為μA=0.2,μB=0.1,g取10m/s2,求:
如圖所示,A、B兩物體的質量分別為mA=0.6kg、mB=0.4kg,放在質量為m車=1kg的足夠長的小車C上,A、B相距8cm,它們隨車以V0=1.0m/s的速度在光滑的水平地面上向右勻速運動,若在小車上加一水平向右的推力F=4N,A、B便在小車上滑動,已知A、B與小車間的動摩擦因數分別為μA=0.2,μB=0.1,g取10m/s2,求:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com