
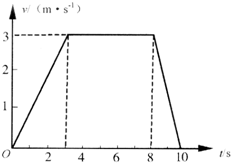
 如圖是某人在一次乘電梯向上運動的v-t圖象.已知g=10m/s2,請根據圖象回答下列問題.
如圖是某人在一次乘電梯向上運動的v-t圖象.已知g=10m/s2,請根據圖象回答下列問題.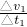 =
=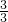 =1m/s2
=1m/s2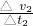 =
=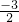 =-1.5m/s2
=-1.5m/s2 (5+10)×3=
(5+10)×3= ×(5+10)×3=22.5m
×(5+10)×3=22.5m
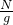 =
=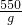 =55kg.
=55kg. gt2
gt2 gt2
gt2 =1.8
=1.8

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中物理 來源: 題型:解答題
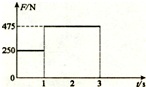 雜技演員在進行“頂桿”表演 時,用的是一根質量為m=10kg的長竹竿.質量為M=30kg的演員自竹竿頂部由靜止開始下滑,滑到竿底時速度恰好為零.已知竿底部與下面頂桿人肩部之間有一力傳感器.竹竿處于靜止狀態,傳感器顯示頂桿人肩部的受力情況如圖所示,g=10m/s2.求:
雜技演員在進行“頂桿”表演 時,用的是一根質量為m=10kg的長竹竿.質量為M=30kg的演員自竹竿頂部由靜止開始下滑,滑到竿底時速度恰好為零.已知竿底部與下面頂桿人肩部之間有一力傳感器.竹竿處于靜止狀態,傳感器顯示頂桿人肩部的受力情況如圖所示,g=10m/s2.求:查看答案和解析>>
科目:高中物理 來源: 題型:單選題
 s
s s
s查看答案和解析>>
科目:高中物理 來源: 題型:多選題
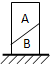 如圖,兩梯形物塊A和B疊放并置于水平地面上處于靜止狀態,則
如圖,兩梯形物塊A和B疊放并置于水平地面上處于靜止狀態,則查看答案和解析>>
科目:高中物理 來源: 題型:多選題
查看答案和解析>>
科目:高中物理 來源: 題型:單選題
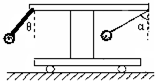 如圖所示,一小車上有一個固定的水平橫桿,左邊有一輕桿與豎直方向成θ角與橫桿固定,下端連接一小鐵球,橫桿右邊用一根細線吊一小鐵球,當小車做勻變速運動時,細線保持與豎直方向成α角,若θ<α,則下列哪一項說法正確的是
如圖所示,一小車上有一個固定的水平橫桿,左邊有一輕桿與豎直方向成θ角與橫桿固定,下端連接一小鐵球,橫桿右邊用一根細線吊一小鐵球,當小車做勻變速運動時,細線保持與豎直方向成α角,若θ<α,則下列哪一項說法正確的是查看答案和解析>>
科目:高中物理 來源: 題型:解答題
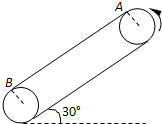 如圖所示,皮帶傳動裝置與水平面夾角為30°,輪半徑R=
如圖所示,皮帶傳動裝置與水平面夾角為30°,輪半徑R=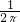 m,兩輪軸心相距L=3.75m,A、B分別使傳送帶與兩輪的切點,輪緣與傳送帶之間不打滑.一個質量為0.1kg的小物塊與傳送帶間的動摩擦因數為μ=
m,兩輪軸心相距L=3.75m,A、B分別使傳送帶與兩輪的切點,輪緣與傳送帶之間不打滑.一個質量為0.1kg的小物塊與傳送帶間的動摩擦因數為μ= .g取10m/s2.
.g取10m/s2.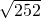 ≈16,
≈16,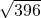 ≈20)
≈20)查看答案和解析>>
科目:高中物理 來源: 題型:解答題
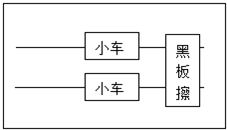 (1)放在光滑水平面上的兩個小車前端各系一根細線,線的另一端跨過定滑輪各掛一個小盤,盤中可放砝碼.小盤和砝碼所受重力,近似等于使小車做勻加速運動的合力,增減小盤中砝碼,可以改變小車受到的合外力.后端各系一根細線,用一個黑板擦把兩根細線同時按在桌上,使小車靜止.抬起黑板擦兩小車同時開始運動,按下黑板擦兩車同時停下,用刻度尺量出兩小車通過的位移.用此辦法驗證牛頓第二定律的實驗中,下列說法正確的是______
(1)放在光滑水平面上的兩個小車前端各系一根細線,線的另一端跨過定滑輪各掛一個小盤,盤中可放砝碼.小盤和砝碼所受重力,近似等于使小車做勻加速運動的合力,增減小盤中砝碼,可以改變小車受到的合外力.后端各系一根細線,用一個黑板擦把兩根細線同時按在桌上,使小車靜止.抬起黑板擦兩小車同時開始運動,按下黑板擦兩車同時停下,用刻度尺量出兩小車通過的位移.用此辦法驗證牛頓第二定律的實驗中,下列說法正確的是______查看答案和解析>>
科目:高中物理 來源: 題型:單選題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com