
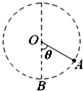
 如圖所示,一小球通過不可伸長的輕繩懸于O點,現(xiàn)從最低點給小球一水平向左的初速度,使小球恰好能在豎直平面內(nèi)做圓周運動,當小球經(jīng)過A點時,其速度為最高點速度的$\sqrt{3}$倍,不計空氣阻力,則在A點輕繩與豎直方向的夾角θ等于( )
如圖所示,一小球通過不可伸長的輕繩懸于O點,現(xiàn)從最低點給小球一水平向左的初速度,使小球恰好能在豎直平面內(nèi)做圓周運動,當小球經(jīng)過A點時,其速度為最高點速度的$\sqrt{3}$倍,不計空氣阻力,則在A點輕繩與豎直方向的夾角θ等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 小球恰好能在豎直平面內(nèi)做圓周運動時,要最高點由重力提供向心力,由牛頓第二定律求出最高點的臨界速度.再由機械能守恒定律分別研究小球從B到最高點及從B到A的過程,聯(lián)立可求得夾角θ.
解答 解:小球剛好通過最高點時,繩子的拉力恰好為零,由牛頓第二定律有:mg=m$\frac{{v}^{2}}{L}$,
解得:v=$\sqrt{gL}$
從最低點到最高點的過程,根據(jù)機械能守恒定律得:
2mgL+$\frac{1}{2}m{v}^{2}$=$\frac{1}{2}m{v}_{B}^{2}$,
解得:vB=$\sqrt{5gL}$
從從B到A的過程,根據(jù)機械能守恒定律得:
$\frac{1}{2}m{v}_{A}^{2}$+mgL(1-cosθ)=$\frac{1}{2}m{v}_{B}^{2}$
據(jù)題有:vA=$\sqrt{3}$v=$\sqrt{3gL}$
聯(lián)立解得:θ=90°
故選:D
點評 解決本題的關鍵知道小球做圓周運動向心力的來源,知道“繩模型”最高點的臨界情況,結合牛頓第二定律和機械能守恒定律進行研究.


科目:高中物理 來源: 題型:解答題
| F/N | 0.5 | 2 | 4.5 | 8 | 12.5 | 18 |
| X/mm | 1 | 2 | 3 | 4 | 5 | 6 |
查看答案和解析>>
科目:高中物理 來源: 題型:解答題
 在光滑絕緣的水平面上有一直角坐標系,現(xiàn)有一個質(zhì)量m=0.1kg、電量為q=+2×10-6C的帶電小球,經(jīng)電勢差U=9000V的加速電場加速后,從y軸正半軸上y=0.6m的 P1處以速度v0沿x軸正方向射入y>0、x>0的空間,在y>0、x>0的空間有沿y軸負方向勻強電場E1,經(jīng)x=1.2m的P2點射入y<0、x>0的空間,在y<0、x>0的空間存在與x軸負方向夾角為45°、大小E2=6$\sqrt{2}$×104V/m勻強電場,從y軸負半軸上的P3點射出.如圖所示,求:
在光滑絕緣的水平面上有一直角坐標系,現(xiàn)有一個質(zhì)量m=0.1kg、電量為q=+2×10-6C的帶電小球,經(jīng)電勢差U=9000V的加速電場加速后,從y軸正半軸上y=0.6m的 P1處以速度v0沿x軸正方向射入y>0、x>0的空間,在y>0、x>0的空間有沿y軸負方向勻強電場E1,經(jīng)x=1.2m的P2點射入y<0、x>0的空間,在y<0、x>0的空間存在與x軸負方向夾角為45°、大小E2=6$\sqrt{2}$×104V/m勻強電場,從y軸負半軸上的P3點射出.如圖所示,求:查看答案和解析>>
科目:高中物理 來源: 題型:多選題
| A. | a=$\frac{△v}{△t}$ | B. | μ=$\frac{{F}_{f}}{{F}_{N}}$ | C. | R=$\frac{L}{s}$ρ | D. | C=$\frac{Q}{U}$ |
查看答案和解析>>
科目:高中物理 來源: 題型:解答題
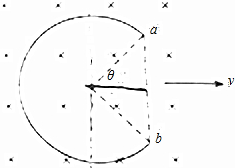 如圖,不閉合的圓形線圈在垂直于磁感應強度為B的勻強磁場的平面內(nèi)平動,速度為v方向垂直于ab連線,設線圈半徑為R,圓心角為θ,則線圈中的感應電動勢為多大?
如圖,不閉合的圓形線圈在垂直于磁感應強度為B的勻強磁場的平面內(nèi)平動,速度為v方向垂直于ab連線,設線圈半徑為R,圓心角為θ,則線圈中的感應電動勢為多大?查看答案和解析>>
科目:高中物理 來源: 題型:解答題
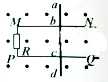 如圖所示兩條光滑水平導軌MN,PQ平行放置,間距為l,其間連接電阻為R,導線abcd電阻也為R,平放在導軌上,ab段和cd段等長,都等于l,導軌電阻不計,整個裝置置于磁感強度為B的勻強磁場中,磁場方向垂直導軌所在的平面向上,當導線abcd以速度v沿導軌方向向右勻速運動時,導線上ad兩點間的電勢差值是多少?
如圖所示兩條光滑水平導軌MN,PQ平行放置,間距為l,其間連接電阻為R,導線abcd電阻也為R,平放在導軌上,ab段和cd段等長,都等于l,導軌電阻不計,整個裝置置于磁感強度為B的勻強磁場中,磁場方向垂直導軌所在的平面向上,當導線abcd以速度v沿導軌方向向右勻速運動時,導線上ad兩點間的電勢差值是多少?查看答案和解析>>
科目:高中物理 來源: 題型:多選題
 如圖所示,將一個質(zhì)量為m的物塊放在水平面上.當用一水平推力F向右推小物塊時,小物塊恰好以一較大的速度勻速運動.某一時刻保持推力的大小不變,并立即使推力反向變?yōu)橄蚝蟮睦Γ瑒t推力反向的瞬間( )
如圖所示,將一個質(zhì)量為m的物塊放在水平面上.當用一水平推力F向右推小物塊時,小物塊恰好以一較大的速度勻速運動.某一時刻保持推力的大小不變,并立即使推力反向變?yōu)橄蚝蟮睦Γ瑒t推力反向的瞬間( )| A. | 小物塊受到的合力大小為2F,方向水平向左 | |
| B. | 小物塊受到的合力大小為2F,方向水平向右 | |
| C. | 地面對小物塊的作用力大小為mg | |
| D. | 地面對小物塊的作用力大小為$\sqrt{{F}^{2}+{m}^{2}{g}^{2}}$ |
查看答案和解析>>
科目:高中物理 來源: 題型:解答題
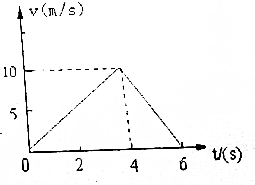 在水平地面上有一質(zhì)量為4千克的物體,在與水平方向成37°角斜向上的恒力F的作下,靜止開始運動.4秒后撤去力F,該物體的速度-時間圖象如圖所示,求
在水平地面上有一質(zhì)量為4千克的物體,在與水平方向成37°角斜向上的恒力F的作下,靜止開始運動.4秒后撤去力F,該物體的速度-時間圖象如圖所示,求查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
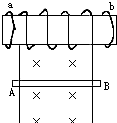 如圖所示,在線圈的左、右兩側分別套上絕緣的金屬環(huán)a、b,在導體AB在勻強磁場中下落的瞬時,a、b環(huán)將( )
如圖所示,在線圈的左、右兩側分別套上絕緣的金屬環(huán)a、b,在導體AB在勻強磁場中下落的瞬時,a、b環(huán)將( )| A. | 向線圈靠攏 | B. | 向兩側跳開 | C. | 一起向左側運動 | D. | 一起向右側運動 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com