
科目: 來源: 題型:
【題目】一款擊鼓小游戲的規則如下:每盤游戲都需擊鼓三次,每次擊鼓后要么出現一次音樂,要么不出現音樂;每盤游戲擊鼓三次后,出現三次音樂獲得150分,出現兩次音樂獲得100分,出現一次音樂獲得50分,沒有出現音樂則獲得-300分.設每次擊鼓出現音樂的概率為![]() ,且各次擊鼓出現音樂相互獨立.
,且各次擊鼓出現音樂相互獨立.
(1)若一盤游戲中僅出現一次音樂的概率為![]() ,求
,求![]() 的最大值點
的最大值點![]() ;
;
(2)以(1)中確定的![]() 作為
作為![]() 的值,玩3盤游戲,出現音樂的盤數為隨機變量
的值,玩3盤游戲,出現音樂的盤數為隨機變量![]() ,求每盤游戲出現音樂的概率
,求每盤游戲出現音樂的概率![]() ,及隨機變量
,及隨機變量![]() 的期望
的期望![]() ;
;
(3)玩過這款游戲的許多人都發現,若干盤游戲后,與最初的分數相比,分數沒有增加反而減少了.請運用概率統計的相關知識分析分數減少的原因.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知拋物線![]() 上一點
上一點![]() 到其焦點下的距離為10.
到其焦點下的距離為10.
(1)求拋物線C的方程;
(2)設過焦點F的的直線![]() 與拋物線C交于
與拋物線C交于![]() 兩點,且拋物線在
兩點,且拋物線在![]() 兩點處的切線分別交x軸于
兩點處的切線分別交x軸于![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目: 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),曲線
為參數),曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以該直角坐標系的原點
為參數),以該直角坐標系的原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,曲線
軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)分別求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設直線![]() 交曲線
交曲線![]() 于
于![]() ,
,![]() 兩點,交曲線
兩點,交曲線![]() 于
于![]() ,
,![]() 兩點,求
兩點,求![]() 的長.
的長.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知a∈R,函數f(x)=(-x2+ax)ex(x∈R).
(1)當a=2時,求函數f(x)的單調區間;
(2)若函數f(x)在(-1,1)上單調遞增,求a的取值范圍.
查看答案和解析>>
科目: 來源: 題型:
【題目】在平面直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為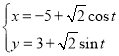 (
(![]() 是參數)以原點
是參數)以原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸,建立極坐標系,直線
軸的非負半軸為極軸,建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求圓![]() 的普通方程和的直線
的普通方程和的直線![]() 直角坐標方程;
直角坐標方程;
(2)設直線![]() 與
與![]() 軸交點分別是
軸交點分別是![]() ,點
,點![]() 是圓
是圓![]() 上的動點,求
上的動點,求![]() 的面積的最小值.
的面積的最小值.
查看答案和解析>>
科目: 來源: 題型:
【題目】離心率為![]() 的橢圓
的橢圓![]() 經過點
經過點![]() ,
,![]() 是坐標原點.
是坐標原點.
(1)求橢圓![]() 的方程;
的方程;
(2)是否存在圓心在原點的圓,使得該圓的任意一條切線與橢圓![]() 恒有兩個交點
恒有兩個交點![]() ,且
,且![]() ?若存在,求出該圓的方程,并求
?若存在,求出該圓的方程,并求![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】2019年9月1日,《西安市生活垃圾分類管理辦法》正式實施.根據規定,生活垃圾分為可回收物、有害垃圾、廚余垃圾和其他垃圾,個人和單位如果不按規定進行垃圾分類將面臨罰款,并納入征信系統.為調查市民對垃圾分類的了解程度,某調查小組隨機抽取了某小區的100位市民,請他們指出生活中若干項常見垃圾的種類,把能準確分類不少于3項的稱為“比較了解”,少于三項的稱為“不太了解”.調查結果如下:
0項 | 1項 | 2項 | 3項 | 4項 | 5項 | 5項以上 | |
男(人) | 1 | 5 | 15 | 8 | 6 | 7 | 3 |
女(人) | 0 | 4 | 11 | 13 | 10 | 12 | 5 |
(1)完成如下![]() 列聯表并判斷是否有99%的把握認為了解垃圾分類與性別有關?
列聯表并判斷是否有99%的把握認為了解垃圾分類與性別有關?
比較了解 | 不太了解 | 合計 | |
男 | |||
女 | |||
合計 |
(2)從對垃圾分類比較了解的市民中用分層抽樣的方式抽取8位,現從這8位市民中隨機選取兩位,求至多有一位男市民的概率.
附: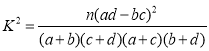
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 來源: 題型:
【題目】棉花的纖維長度是棉花質量的重要指標.在一批棉花中抽測了60根棉花的纖維長度(單位:![]() ),將樣本數據制作成如下的頻率分布直方圖:
),將樣本數據制作成如下的頻率分布直方圖:
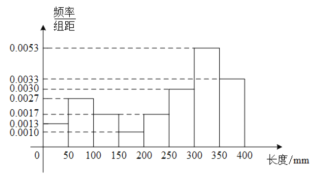
下列關于這批棉花質量狀況的分析不正確的是( )
A.纖維長度在![]() 的棉花的數量為9根
的棉花的數量為9根
B.從這60根棉花中隨機選取1根,其纖維長度在![]() 的概率為0.335
的概率為0.335
C.有超過一半的棉花纖維長度能達到![]() 以上
以上
D.這批棉花的纖維長度的中位數的估計值為![]() .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】某地區高考實行新方案,規定:語文、數學和英語是考生的必考科目,考生還須從物理、化學、生物、歷史、地理和政治六個科目中選取三個科目作為選考科目.若一個學生從六個科目中選出了三個科目作為選考科目,則稱該學生的選考方案確定;否則,稱該學生選考方案待確定.例如,學生甲選擇“物理、化學和生物”三個選考科目,則學生甲的選考方案確定,“物理、化學和生物”為其選考方案.
某學校為了解高一年級420名學生選考科目的意向,隨機選取30名學生進行了一次調查,統計選考科目人數如下表:
性別 | 選考方案確定情況 | 物理 | 化學 | 生物 | 歷史 | 地理 | 政治 |
男生 | 選考方案確定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
選考方案待確定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 選考方案確定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
選考方案待確定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
(1)估計該學校高一年級選考方案確定的學生中選考生物的學生有多少人?
(2)假設男生、女生選擇選考科目是相互獨立的.從選考方案確定的8位男生中隨機選出1人,從選考方案確定的10位女生中隨機選出1人,試求該男生和該女生的選考方案中都含有歷史學科的概率;
(3)從選考方案確定的8名男生中隨機選出2名,設隨機變量 求
求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知橢圓![]() 的中心在原點
的中心在原點![]() ,焦點在
,焦點在![]() 軸上,左右焦點分別為
軸上,左右焦點分別為![]() ,
,![]() ,離心率為
,離心率為![]() ,右焦點到右頂點的距離為1.
,右焦點到右頂點的距離為1.
(1)求橢圓![]() 的方程;
的方程;
(2)過![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,
,![]() ,則
,則![]() 的面積是否存在最大值?若存在,求出這個最大值及直線
的面積是否存在最大值?若存在,求出這個最大值及直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com