
科目: 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為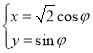 (
(![]() 為參數(shù)),以坐標(biāo)原點
為參數(shù)),以坐標(biāo)原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線![]() 的極坐標(biāo)方程和
的極坐標(biāo)方程和![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)![]() 是曲線
是曲線![]() 上一點,此時參數(shù)
上一點,此時參數(shù)![]() ,將射線
,將射線![]() 繞原點
繞原點![]() 逆時針旋轉(zhuǎn)
逆時針旋轉(zhuǎn)![]() 交曲線
交曲線![]() 于點
于點![]() ,記曲線
,記曲線![]() 的上頂點為點
的上頂點為點![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知橢圓![]() 的一個焦點與拋物線
的一個焦點與拋物線![]() 的焦點重合,且橢圓
的焦點重合,且橢圓![]() 的離心率為
的離心率為![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,直線
,直線![]() 是線段
是線段![]() 的垂直平分線,求證:直線
的垂直平分線,求證:直線![]() 過定點,并求出該定點的坐標(biāo).
過定點,并求出該定點的坐標(biāo).
查看答案和解析>>
科目: 來源: 題型:
【題目】某醫(yī)院治療白血病有甲、乙兩套方案,現(xiàn)就70名患者治療后復(fù)發(fā)的情況進行了統(tǒng)計,得到其等高條形圖如圖所示(其中采用甲、乙兩種治療方案的患者人數(shù)之比為![]() .
.
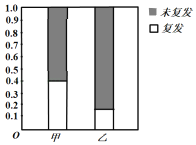
(1)補充完整![]() 列聯(lián)表中的數(shù)據(jù),并判斷是否有
列聯(lián)表中的數(shù)據(jù),并判斷是否有![]() 把握認為甲乙兩套治療方案對患者白血病復(fù)發(fā)有影響;
把握認為甲乙兩套治療方案對患者白血病復(fù)發(fā)有影響;
復(fù)發(fā) | 未復(fù)發(fā) | 總計 | |
甲方案 | |||
乙方案 | 2 | ||
總計 | 70 |
(2)為改進“甲方案”,按分層抽樣組成了由5名患者構(gòu)成的樣本,求隨機抽取2名患者恰好是復(fù)發(fā)患者和未復(fù)發(fā)患者各1名的概率.
附:
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 |
![]() ,
,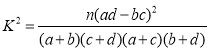 .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】根據(jù)有關(guān)資料預(yù)測,某市下月1—14日的空氣質(zhì)量指數(shù)趨勢如下圖所示.,根據(jù)已知折線圖,解答下面的問題:
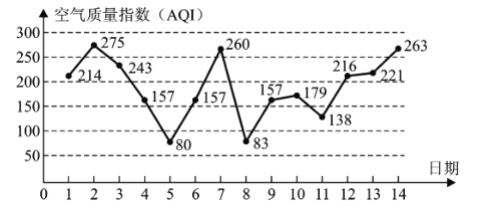
(1)求污染指數(shù)的眾數(shù)及前五天污染指數(shù)的平均值;(保留整數(shù))
(2)為了更好發(fā)揮空氣質(zhì)量監(jiān)測服務(wù)人民的目的,監(jiān)測部門在發(fā)布空氣質(zhì)量指數(shù)的同時,也給出了出行建議,比如空氣污染指數(shù)大于150時需要戴口罩,超過200時建議減少外出活動等等.如果某人事先沒有注意到空氣質(zhì)量預(yù)報,而在1—12號這12天中隨機選定一天,欲在接下來的兩天中(不含選定當(dāng)天)進行外出活動.求其外出活動的兩天期間.
①恰好都遭遇重度及以上污染天氣的概率;
②至少有一天能避開重度及以上污染天氣的概率.
附:空氣質(zhì)量等級參考表:
|
|
|
|
|
|
|
等級 | 優(yōu) | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
查看答案和解析>>
科目: 來源: 題型:
【題目】下列說法不正確的是( )
A.“![]() 為真”是“
為真”是“![]() 為真”的充分不必要條件;
為真”的充分不必要條件;
B.若數(shù)據(jù)![]() 的平均數(shù)為1,則
的平均數(shù)為1,則![]() 的平均數(shù)為2;
的平均數(shù)為2;
C.在區(qū)間![]() 上隨機取一個數(shù)
上隨機取一個數(shù)![]() ,則事件“
,則事件“![]() ”發(fā)生的概率為
”發(fā)生的概率為![]()
D.設(shè)從總體中抽取的樣本為![]() 若記樣本橫、縱坐標(biāo)的平均數(shù)分別為
若記樣本橫、縱坐標(biāo)的平均數(shù)分別為![]() ,則回歸直線
,則回歸直線![]() 必過點
必過點![]()
查看答案和解析>>
科目: 來源: 題型:
【題目】某大型公司為了切實保障員工的健康安全,貫徹好衛(wèi)生防疫工作的相關(guān)要求,決定在全公司范圍內(nèi)舉行一次乙肝普查.為此需要抽驗960人的血樣進行化驗,由于人數(shù)較多,檢疫部門制定了下列兩種可供選擇的方案.方案①:將每個人的血分別化驗,這時需要驗960次.方案②:按![]() 個人一組進行隨機分組,把從每組
個人一組進行隨機分組,把從每組![]() 個人抽來的血混合在一起進行檢驗,如果每個人的血均為陰性,則驗出的結(jié)果呈陰性,這
個人抽來的血混合在一起進行檢驗,如果每個人的血均為陰性,則驗出的結(jié)果呈陰性,這![]() 個人的血就只需檢驗一次(這時認為每個人的血化驗
個人的血就只需檢驗一次(這時認為每個人的血化驗![]() 次);否則,若呈陽性,則需對這
次);否則,若呈陽性,則需對這![]() 個人的血樣再分別進行一次化驗.這樣,該組
個人的血樣再分別進行一次化驗.這樣,該組![]() 個人的血總共需要化驗
個人的血總共需要化驗![]() 次.假設(shè)此次普查中每個人的血樣化驗呈陽性的概率為
次.假設(shè)此次普查中每個人的血樣化驗呈陽性的概率為![]() ,且這些人之間的試驗反應(yīng)相互獨立.
,且這些人之間的試驗反應(yīng)相互獨立.
(1)設(shè)方案②中,某組![]() 個人中每個人的血化驗次數(shù)為
個人中每個人的血化驗次數(shù)為![]() ,求
,求![]() 的分布列;
的分布列;
(2)設(shè)![]() .試比較方案②中,
.試比較方案②中,![]() 分別取2,3,4時,各需化驗的平均總次數(shù);并指出在這三種分組情況下,相比方案①,化驗次數(shù)最多可以平均減少多少次?(最后結(jié)果四舍五入保留整數(shù)).
分別取2,3,4時,各需化驗的平均總次數(shù);并指出在這三種分組情況下,相比方案①,化驗次數(shù)最多可以平均減少多少次?(最后結(jié)果四舍五入保留整數(shù)).
查看答案和解析>>
科目: 來源: 題型:
【題目】設(shè)橢圓![]() 的一個焦點為
的一個焦點為![]() ,四條直線
,四條直線![]() ,
,![]() 所圍成的區(qū)域面積為
所圍成的區(qū)域面積為![]() .
.
(1)求![]() 的方程;
的方程;
(2)設(shè)過![]() 的直線
的直線![]() 與
與![]() 交于不同的兩點
交于不同的兩點![]() ,設(shè)弦
,設(shè)弦![]() 的中點為
的中點為![]() ,且
,且![]() (
(![]() 為原點),求直線
為原點),求直線![]() 的方程.
的方程.
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,幾何體![]() 中,
中,![]() ,
,![]() 均為邊長為2的正三角形,且平面
均為邊長為2的正三角形,且平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 為正方形.
為正方形.
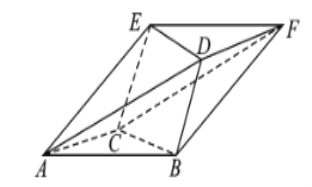
(1)若平面![]() 平面
平面![]() ,求證:平面
,求證:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 為
為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com