
科目: 來源: 題型:
【題目】已知線段![]() 是過拋物線
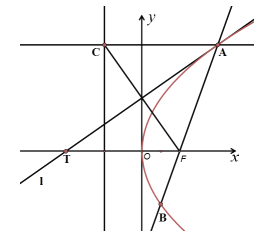
是過拋物線![]() 的焦點F的一條弦,過點A(A在第一象限內)作直線
的焦點F的一條弦,過點A(A在第一象限內)作直線![]() 垂直于拋物線的準線,垂足為C,直線
垂直于拋物線的準線,垂足為C,直線![]() 與拋物線相切于點A,交x軸于點T,給出下列命題:
與拋物線相切于點A,交x軸于點T,給出下列命題:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() .
.
其中正確的命題個數為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 來源: 題型:
【題目】下圖統計了截止到2019年年底中國電動汽車充電樁細分產品占比及保有量情況,關于這5次統計,下列說法正確的是( )
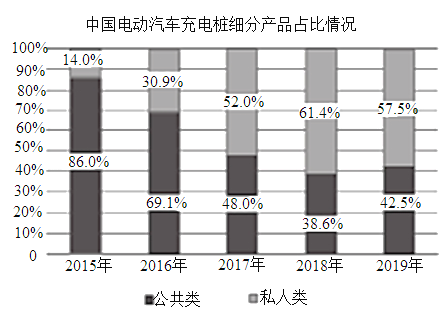
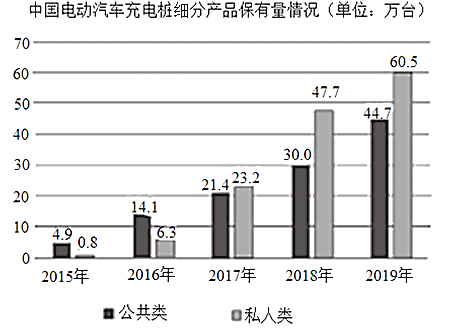
A.私人類電動汽車充電樁保有量增長率最高的年份是2018年
B.公共類電動汽車充電樁保有量的中位數是25.7萬臺
C.公共類電動汽車充電樁保有量的平均數為23.12萬臺
D.從2017年開始,我國私人類電動汽車充電樁占比均超過50%
查看答案和解析>>
科目: 來源: 題型:
【題目】《算法統宗》是中國古代數學名著,由明代數學家程大位編著,它對我國民間普及珠算和數學知識起到了很大的作用,是東方古代數學的名著.在這部著作中,許多數學問題都是以歌訣形式呈現的,“九兒問甲歌”就是其中一首:“一個公公九個兒,若問生年總不知,自長排來差三歲,共年二百又零七,借問長兒多少歲,各兒歲數要詳推.”這首歌決的大意是:“一位老公公有九個兒子,九個兒子從大到小排列,相鄰兩人的年齡差三歲,并且兒子們的年齡之和為207歲,請問大兒子多少歲,其他幾個兒子年齡如何推算.”在這個問題中,記這位公公的第![]() 個兒子的年齡為
個兒子的年齡為![]() ,則
,則![]() ( )
( )
A.17B.29C.23D.35
查看答案和解析>>
科目: 來源: 題型:
【題目】設橢圓![]() 的左頂點為
的左頂點為![]() ,右頂點為
,右頂點為![]() ,已知橢圓
,已知橢圓![]() 的離心率為
的離心率為![]() ,且以線段
,且以線段![]() 為直徑的圓被直線
為直徑的圓被直線![]() 所截的弦長為
所截的弦長為![]() .
.
(1)求橢圓的方程;
(2)記橢圓![]() 的右焦點為
的右焦點為![]() ,過點
,過點![]() 且斜率為
且斜率為![]() 的直線交橢圓于
的直線交橢圓于![]() 兩點.若線段
兩點.若線段![]() 的垂直平分線與
的垂直平分線與![]() 軸交于點
軸交于點![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目: 來源: 題型:
【題目】為貫徹落實黨中央全面建設小康社會的戰略部署,某貧困地區的廣大黨員干部深入農村積極開展“精準扶貧”工作.經過多年的精心幫扶,截至2018年底,按照農村家庭人均年純收入8000元的小康標準,該地區僅剩部分家庭尚未實現小康,2019年6月,為估計該地能否在2020年全面實現小康,統計了該地當時最貧困的一個家庭2019年1至6月的人均月純收入,作出散點如下:
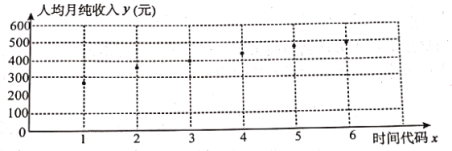
根據盯關性分析,發現其家庭人均月純收入![]() 與時間代碼
與時間代碼![]() 之間具有較強的線性相關關系(記2019年1月、2月……分別為
之間具有較強的線性相關關系(記2019年1月、2月……分別為![]() ,
,![]() ,…,依此類推),由此估計該家庭2020年能實現小康生活.但2020年1月突如其來的新冠肺炎疫情影響了奔小康的進展,該家庭2020年第一季度每月的人均月純收入只有2019年12月的預估值的
,…,依此類推),由此估計該家庭2020年能實現小康生活.但2020年1月突如其來的新冠肺炎疫情影響了奔小康的進展,該家庭2020年第一季度每月的人均月純收入只有2019年12月的預估值的![]() .
.
(1)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)求該家庭2020年3月份的人均月純收入;
(3)如果以該家庭3月份人均月純收入為基數,以后每月增長率為![]() ,問該家庭2020年底能否實現小康生活?
,問該家庭2020年底能否實現小康生活?
參考數據:![]() ,
,![]() ,
,![]()
參考公式: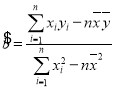 ,
,![]() .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】謝賓斯基三角形是一種分形,由波蘭數學家謝賓斯基在1915年提出,先作一個正三角形挖去一個“中心三角形”(即以原三角形各邊的中點為頂點的三角形),然后在剩下的小三角形中又挖去一個“中心三角形”,我們用白色代表挖去的面積,那么黑三角形為剩下的面積(我們稱黑三角形為謝賓斯基三角形).向圖中第4個大正三角形中隨機撒512粒大小均勻的細小顆粒物,則落在白色區域的細小顆粒物的數量約是( )
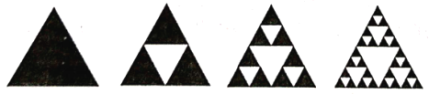
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 來源: 題型:
【題目】某工廠生產某種電子產品,每件產品合格的概率均為![]() ,現工廠為提高產品聲譽,要求在交付用戶前每件產品都通過合格檢驗,已知該工廠的檢驗儀器一次最多可檢驗
,現工廠為提高產品聲譽,要求在交付用戶前每件產品都通過合格檢驗,已知該工廠的檢驗儀器一次最多可檢驗![]() 件該產品,且每件產品檢驗合格與否相互獨立.若每件產品均檢驗一次,所需檢驗費用較多,該工廠提出以下檢驗方案:將產品每
件該產品,且每件產品檢驗合格與否相互獨立.若每件產品均檢驗一次,所需檢驗費用較多,該工廠提出以下檢驗方案:將產品每![]() 個(
個(![]() )一組進行分組檢驗,如果某一組產品檢驗合格,則說明該組內產品均合格,若檢驗不合格,則說明該組內有不合格產品,再對該組內每一件產品單獨進行檢驗,如此,每一組產品只需檢驗一次或
)一組進行分組檢驗,如果某一組產品檢驗合格,則說明該組內產品均合格,若檢驗不合格,則說明該組內有不合格產品,再對該組內每一件產品單獨進行檢驗,如此,每一組產品只需檢驗一次或![]() 次.設該工廠生產
次.設該工廠生產![]() 件該產品,記每件產品的平均檢驗次數為
件該產品,記每件產品的平均檢驗次數為![]() .
.
(1)![]() 的分布列及其期望;
的分布列及其期望;
(2)(i)試說明,當![]() 越大時,該方案越合理,即所需平均檢驗次數越少;
越大時,該方案越合理,即所需平均檢驗次數越少;
(ii)當![]() 時,求使該方案最合理時
時,求使該方案最合理時![]() 的值及
的值及![]() 件該產品的平均檢驗次數.
件該產品的平均檢驗次數.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知橢圓![]() 的離心率
的離心率![]() ,橢圓
,橢圓![]() 上的點到其左焦點
上的點到其左焦點![]() 的最大距離為
的最大距離為![]() .
.
(1)求橢圓的標準方程;
(2)過橢圓![]() 左焦點
左焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,直線
兩點,直線![]() ,過點
,過點![]() 作直線
作直線![]() 的垂線與直線
的垂線與直線![]() 交于點
交于點![]() ,求
,求![]() 的最小值和此時直線
的最小值和此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目: 來源: 題型:
【題目】波羅尼斯(古希臘數學家,約公元前262-190年)的著作《圓錐曲線論》是古代世界光輝的科學成果,它將圓錐曲線的性質網羅殆盡幾乎使后人沒有插足的余地.他證明過這樣一個命題:平面內與兩定點距離的比為常數k(![]() 且
且![]() )的點的軌跡是圓,后人將這個圓稱為阿波羅尼斯圓.現有
)的點的軌跡是圓,后人將這個圓稱為阿波羅尼斯圓.現有![]() ,
,![]() ,則當
,則當![]() 的面積最大時,AC邊上的高為_______________.
的面積最大時,AC邊上的高為_______________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com