
【題目】某工廠生產某種電子產品,每件產品合格的概率均為![]() ,現工廠為提高產品聲譽,要求在交付用戶前每件產品都通過合格檢驗,已知該工廠的檢驗儀器一次最多可檢驗
,現工廠為提高產品聲譽,要求在交付用戶前每件產品都通過合格檢驗,已知該工廠的檢驗儀器一次最多可檢驗![]() 件該產品,且每件產品檢驗合格與否相互獨立.若每件產品均檢驗一次,所需檢驗費用較多,該工廠提出以下檢驗方案:將產品每
件該產品,且每件產品檢驗合格與否相互獨立.若每件產品均檢驗一次,所需檢驗費用較多,該工廠提出以下檢驗方案:將產品每![]() 個(
個(![]() )一組進行分組檢驗,如果某一組產品檢驗合格,則說明該組內產品均合格,若檢驗不合格,則說明該組內有不合格產品,再對該組內每一件產品單獨進行檢驗,如此,每一組產品只需檢驗一次或
)一組進行分組檢驗,如果某一組產品檢驗合格,則說明該組內產品均合格,若檢驗不合格,則說明該組內有不合格產品,再對該組內每一件產品單獨進行檢驗,如此,每一組產品只需檢驗一次或![]() 次.設該工廠生產
次.設該工廠生產![]() 件該產品,記每件產品的平均檢驗次數為
件該產品,記每件產品的平均檢驗次數為![]() .
.
(1)![]() 的分布列及其期望;
的分布列及其期望;
(2)(i)試說明,當![]() 越大時,該方案越合理,即所需平均檢驗次數越少;
越大時,該方案越合理,即所需平均檢驗次數越少;
(ii)當![]() 時,求使該方案最合理時
時,求使該方案最合理時![]() 的值及
的值及![]() 件該產品的平均檢驗次數.
件該產品的平均檢驗次數.
【答案】(1)分布列詳見解析,期望![]() ;(2)(i)詳見解析;(ii)
;(2)(i)詳見解析;(ii)![]() 時平均檢驗次數最少,約
時平均檢驗次數最少,約![]() 次.
次.
【解析】
(1)根據每![]() 個(
個(![]() )一組進行分組檢驗,如果某一組產品檢驗合格,則說明該組內產品均合格,若檢驗不合格,則說明該組內有不合格產品,再對該組內每一件產品單獨進行檢驗,如此,每一組產品只需檢驗一次或
)一組進行分組檢驗,如果某一組產品檢驗合格,則說明該組內產品均合格,若檢驗不合格,則說明該組內有不合格產品,再對該組內每一件產品單獨進行檢驗,如此,每一組產品只需檢驗一次或![]() 次,每件產品的平均檢驗次數
次,每件產品的平均檢驗次數![]() 的可能取值為
的可能取值為![]() ,
,![]() ,再利用獨立事件和互斥事件求得概率列出分布列,再求期望
,再利用獨立事件和互斥事件求得概率列出分布列,再求期望
(2)(i)由(1)知![]() ,根據指數函數的單調性得到
,根據指數函數的單調性得到![]() 在
在![]() 上單調遞減,從而得到結論. (ii)由(1)記
上單調遞減,從而得到結論. (ii)由(1)記![]() ,則由
,則由![]() 且取最小值時,該方案最合理求解.
且取最小值時,該方案最合理求解.
(1)由題意,![]() 的可能取值為
的可能取值為![]() ,
,![]()
![]() ,
,![]() ,
,
故![]() 的分布列為
的分布列為
|
|
|
|
|
|
![]()
(2)(i)由(1),記![]() ,
,
因為![]() .所以
.所以![]() 在
在![]() 上單調遞減,
上單調遞減,
故![]() 越大,
越大,![]() 越小,即所需平均檢驗次數越少,該方案越合理.
越小,即所需平均檢驗次數越少,該方案越合理.
(ii)記![]() ,當
,當![]() 且取最小值時,該方案最合理,
且取最小值時,該方案最合理,
因為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() 時平均檢驗次數最少,約
時平均檢驗次數最少,約![]() 次.
次.


科目:高中數學 來源: 題型:
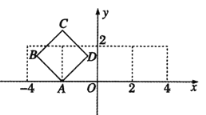
【題目】在平面直角坐標系![]() 中,如圖放置的邊長為2的正方形ABCD沿
中,如圖放置的邊長為2的正方形ABCD沿![]() 軸滾動(無滑動滾動),點D恰好經過坐標原點,設頂點
軸滾動(無滑動滾動),點D恰好經過坐標原點,設頂點![]() 的軌跡方程是
的軌跡方程是![]() ,則對函數
,則對函數![]() 的判斷正確的是( )
的判斷正確的是( )
A.函數![]() 在
在![]() 上有兩個零點
上有兩個零點
B.函數![]() 是偶函數
是偶函數
C.函數![]() 在
在![]() 上單調遞增
上單調遞增
D.對任意的![]() ,都有
,都有![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三棱錐![]() 中,頂點
中,頂點![]() 在底面
在底面![]() 的投影為
的投影為![]() 的內心,三個側面的面積分別為12,16,20,且底面面積為24,則三棱錐
的內心,三個側面的面積分別為12,16,20,且底面面積為24,則三棱錐![]() 的內切球的表面積為( )
的內切球的表面積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
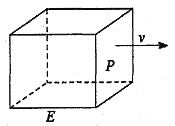
【題目】如圖,長方形物體E在雨中沿面P(面積為S)的垂直方向作勻速移動,速度為![]() ,雨速沿E移動方向的分速度為
,雨速沿E移動方向的分速度為![]() 。E移動時單位時間內的淋雨量包括兩部分:(1)P或P的平行面(只有一個面淋雨)的淋雨量,假設其值與
。E移動時單位時間內的淋雨量包括兩部分:(1)P或P的平行面(只有一個面淋雨)的淋雨量,假設其值與![]() ×S成正比,比例系數為
×S成正比,比例系數為![]() ;(2)其它面的淋雨量之和,其值為
;(2)其它面的淋雨量之和,其值為![]() ,記
,記![]() 為E移動過程中的總淋雨量,當移動距離d=100,面積S=
為E移動過程中的總淋雨量,當移動距離d=100,面積S=![]() 時。
時。
(1)寫出![]() 的表達式
的表達式
(2)設0<v≤10,0<c≤5,試根據c的不同取值范圍,確定移動速度![]() ,使總淋雨量
,使總淋雨量![]() 最少。
最少。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖統計了截止到2019年年底中國電動汽車充電樁細分產品占比及保有量情況,關于這5次統計,下列說法正確的是( )
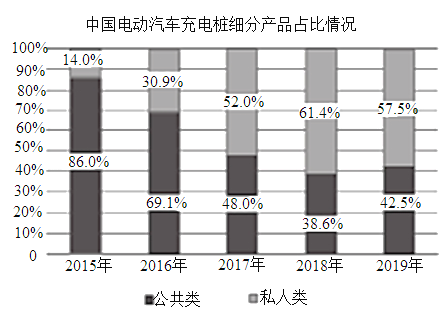
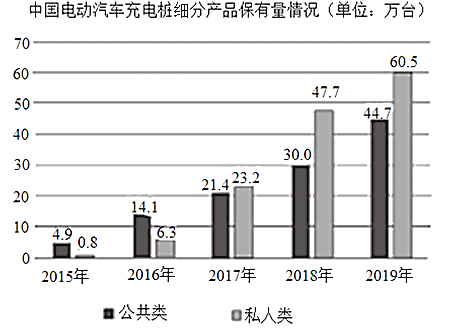
A.私人類電動汽車充電樁保有量增長率最高的年份是2018年
B.公共類電動汽車充電樁保有量的中位數是25.7萬臺
C.公共類電動汽車充電樁保有量的平均數為23.12萬臺
D.從2017年開始,我國私人類電動汽車充電樁占比均超過50%
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年,泉州市區的房價依舊是市民關心的話題.總體來說,二手房房價有所下降;相比二手房而言,新房市場依然強勁,價格持續升高.已知銷售人員主要靠售房提成領取工資.現統計泉州市某新房銷售人員2019年一年的工資情況的結果如圖所示,則下列說法正確的是( )
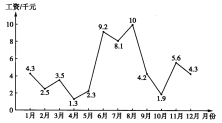
A.2019年該銷售人員月工資的中位數為![]()
B.2019年該銷售人員8月份的工資增長率最高
C.2019年該銷售人員第一季度月工資的方差小于第二季度月工資的方差
D.2019年該銷售人員第一季度月工資的平均數大于第四季度月工資的平均數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知O為原點,拋物線![]() 的準線與y軸的交點為H,P為拋物線C上橫坐標為4的點,已知點P到準線的距離為5.
的準線與y軸的交點為H,P為拋物線C上橫坐標為4的點,已知點P到準線的距離為5.
(1)求C的方程;
(2)過C的焦點F作直線l與拋物線C交于A,B兩點,若以AH為直徑的圓過B,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com