
科目: 來源:[同步]2014年北師大版選修1-2 3.2數學證明練習卷(解析版) 題型:選擇題
(2014•天津一模)定義一種新運算:a?b=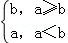 ,已知函數f(x)=(1+
,已知函數f(x)=(1+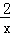 )?3log2(x+1),若方程f(x)﹣k=0恰有兩個不相等的實根,則實數k的取值范圍為( )
)?3log2(x+1),若方程f(x)﹣k=0恰有兩個不相等的實根,則實數k的取值范圍為( )
A.(﹣∞,3)
B.(1,3)
C.(﹣∞,﹣3)∪(1,3)
D.(﹣∞,﹣3)∪(0,3)
查看答案和解析>>
科目: 來源:[同步]2014年北師大版選修1-2 3.2數學證明練習卷(解析版) 題型:選擇題
(2014•天津二模)在實數集R中定義一種運算“⊕”,具有性質:
①對?a,b∈R,a⊕b=b⊕a;
②對?a∈R,a⊕0=a;
③對?a,b,c∈R,(a⊕b)⊕c=c⊕(ab)+(a⊕c)+(b⊕c)﹣2c;
那么函數f(x)=x⊕ (x≥1)的最小值為( )
(x≥1)的最小值為( )
A.5 B.4 C.2+2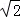 D.2
D.2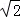
查看答案和解析>>
科目: 來源:[同步]2014年北師大版選修1-2 3.2數學證明練習卷(解析版) 題型:選擇題
(2014•泉州模擬)若函數y=f(x)滿足:集合A={f(n)|n∈N*}中至少有三個不同的數成等差數列,則稱函數f(x)是“等差源函數”,則下列四個函數中,“等差源函數”的個數是( )
①y=2x+1;
②y=log2x;
③y=2x+1;
④y=sin( x+
x+ )
)
A.1 B.2 C.3 D.4
查看答案和解析>>
科目: 來源:[同步]2014年北師大版選修1-2 3.2數學證明練習卷(解析版) 題型:選擇題
(2014•榆林模擬)甲,乙,丙,丁,戊5名學生進行某種勞動技術比賽決出第1名到第5名的名次(無并列).甲乙兩名參賽者去詢問成績,回答者對甲說“很遺憾,你和乙都沒有得到冠軍”;對乙說“你當然不是最差的”.從這個人的回答中分析,5人的名次情況共有( )種.
A.54 B.48 C.36 D.72
查看答案和解析>>
科目: 來源:[同步]2014年北師大版選修1-2 3.2數學證明練習卷(解析版) 題型:選擇題
(2014•郴州三模)設集合A⊆R,如果x0∈R滿足:對任意a>0,都存在x∈A,使得0<|x﹣x0|<a,那么稱x0為集合A的一個聚點.則在下列集合中:
(1)Z+∪Z﹣;
(2)R+∪R﹣;
(3){x|x= ,n∈N*};
,n∈N*};
(4){x|x=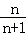 ,n∈N*}.
,n∈N*}.
其中以0為聚點的集合有( )
A.1個 B.2個 C.3個 D.4個
查看答案和解析>>
科目: 來源:[同步]2014年北師大版選修1-2 3.2數學證明練習卷(解析版) 題型:選擇題
(2014•陜西模擬)已知[x]表示不超過實數x的最大整數(x∈R),如:[﹣1,3]=﹣2,[0.8]=0,[3,4]=3.定義{x}=x﹣[x],求{ }+{
}+{ }+{
}+{ }+…+{
}+…+{ }=( )
}=( )
A.2013 B. C.1007 D.2014
C.1007 D.2014
查看答案和解析>>
科目: 來源:[同步]2014年北師大版選修1-2 3.2數學證明練習卷(解析版) 題型:選擇題
(2014•陜西模擬)已知[x]表示不超過實數x的最大整數(x∈R),如:[﹣1.3]=﹣2,[0.8]=0,[3.4]=3.定義{x}=x﹣[x],求{ }+{
}+{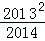 }+{
}+{ }+…+{
}+…+{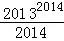 }=( )
}=( )
A.1006 B.1007 C.1008 D.2014
查看答案和解析>>
科目: 來源:[同步]2014年北師大版選修1-2 3.3綜合法與分析法練習卷(解析版) 題型:選擇題
(2014•合肥一模)對于函數f(x),若?a,b,c∈R,f(a),f(b),f(c)都是某一三角形的三邊長,則稱f(x)為“可構造三角形函數”.以下說法正確的是( )
A.f(x)=1(x∈R)不是“可構造三角形函數”
B.“可構造三角形函數”一定是單調函數
C.f(x)=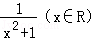 是“可構造三角形函數”
是“可構造三角形函數”
D.若定義在R上的函數f(x)的值域是 (e為自然對數的底數),則f(x)一定是“可構造三角形函數”
(e為自然對數的底數),則f(x)一定是“可構造三角形函數”
查看答案和解析>>
科目: 來源:[同步]2014年北師大版選修1-2 3.3綜合法與分析法練習卷(解析版) 題型:選擇題
證明命題:“f(x)=ex+ 在(0,+∞)上是增函數”,現給出的證法如下:
在(0,+∞)上是增函數”,現給出的證法如下:
因為f(x)=ex+ ,所以f′(x)=ex﹣
,所以f′(x)=ex﹣ ,
,
因為x>0,所以ex>1,0< <1,
<1,
所以ex﹣ >0,即f′(x)>0,
>0,即f′(x)>0,
所以f(x)在(0,+∞)上是增函數,使用的證明方法是( )
A.綜合法 B.分析法 C.反證法 D.以上都不是
查看答案和解析>>
科目: 來源:[同步]2014年北師大版選修1-2 3.3綜合法與分析法練習卷(解析版) 題型:選擇題
分析法是從要證的不等式出發,尋求使它成立的( )
A.充分條件 B.必要條件
C.充要條件 D.既不充分又不必要條件
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com