毛片在线视频,午夜视频,亚洲一区中文

相關習題

0 198687 198695 198701 198705 198711 198713 198717 198723 198725 198731 198737 198741 198743 198747 198753 198755 198761 198765 198767 198771 198773 198777 198779 198781 198782 198783 198785 198786 198787 198789 198791 198795 198797 198801 198803 198807 198813 198815 198821 198825 198827 198831 198837 198843 198845 198851 198855 198857 198863 198867 198873 198881 266669

科目： 來源： 題型：

下列結(jié)論中不正確的是（　　）

A、（2，

）與（2，-

）關于極軸對稱

B、（2，

）與（2，

7π

）是關于極點對稱

C、（2，

）與（-2，

5π

）是關于極軸對稱

D、（2，

）與（-2，-

5π

）是關于極點對稱

查看答案和解析>>

科目： 來源： 題型：

若點P的直角坐標為（-

，1），以點P所在的直角坐標系的原點為極點，x軸的正方向為極軸，建立極坐標系．則點P的極坐標為（　　）

A、（2，

2π

）

B、（2，

5π

）

C、（2，

）

D、（2，

）

查看答案和解析>>

科目： 來源： 題型：

已知點P的直角坐標為（-1，-1），則點P的極坐標可能為（　　）

A、（

，

）

B、（

，

π）

C、（

，

π）

D、（

，

7π

）

查看答案和解析>>

科目： 來源： 題型：

在極坐標系中，以極點為坐標原點，極軸為x軸正半軸，建立直角坐標系，點M（2，

）的直角坐標是（　　）

A、（2，1）

B、（

，1）

C、（1，

）

D、（1，2）

查看答案和解析>>

科目： 來源： 題型：

在極坐標系中與點A（6，

4π

）重合的點是（　　）

A、（6，

）

B、（6，

7π

）

C、（-6，

）

D、（-6，

2π

）

查看答案和解析>>

科目： 來源： 題型：

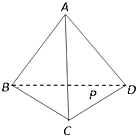如圖，設P為正四面體A-BCD表面（含棱）上與頂點不重合的一點，由點P到四個頂點的距離組成的集合記為M，如果集合M中有且只有2個元素，那么符合條件的點P有（　　）

A、4個	B、6個
C、10個	D、14個

查看答案和解析>>

科目： 來源： 題型：

6把椅子排成一排，3人隨機就座，任何兩人不相鄰的坐法種數(shù)為（　　）

A、144	B、120
C、72	D、24

查看答案和解析>>

科目： 來源： 題型：

已知曲線C：y=

和直線：x-2y=0由C與圍成封閉圖形記為M．
（1）求M的面積；
（2）若M繞x軸旋轉(zhuǎn)一周，求由M圍成的體積．

查看答案和解析>>

科目： 來源： 題型：

由拋物線y²=2x與直線x=1及x軸所圍成的圖形繞x軸旋轉(zhuǎn)一周所得旋轉(zhuǎn)體的體積

．

查看答案和解析>>

科目： 來源： 題型：

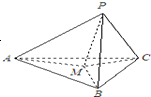如圖，在三棱錐P-ABC中，PA、PB、PC兩兩垂直，且PA=3，PB=2，PC=2．設M是底面ABC內(nèi)一點，定義f（M）=（m，n，p），其中m、n、p分別是三棱錐M-PAB、三棱錐M-PBC、三棱錐M-PCA的體積．若f（M）=（

，x，y），則

的最小值是

．

查看答案和解析>>

同步練習冊答案

日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

練習冊

高中

初中

小學