相關習題
0 108869 108877 108883 108887 108893 108895 108899 108905 108907 108913 108919 108923 108925 108929 108935 108937 108943 108947 108949 108953 108955 108959 108961 108963 108964 108965 108967 108968 108969 108971 108973 108977 108979 108983 108985 108989 108995 108997 109003 109007 109009 109013 109019 109025 109027 109033 109037 109039 109045 109049 109055 109063 266669
科目:
來源:2011年《龍門亮劍》高三數學(理科)一輪復習:第2章第10節(人教AB通用)(解析版)
題型:選擇題
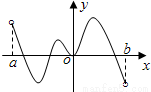
函數f(x)的定義域為開區間(a,b),導函數f′(x)在(a,b)內的圖象如圖所示,則函數f(x)在開區間(a,b)內有極小值點的個數為( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:
來源:2011年《龍門亮劍》高三數學(理科)一輪復習:第2章第10節(人教AB通用)(解析版)
題型:選擇題
設a∈R,若函數y=e
ax+3x,x∈R有大于零的極值點,則( )
A.a>-3
B.a<-3
C.a>-

D.a<-

查看答案和解析>>
科目:
來源:2011年《龍門亮劍》高三數學(理科)一輪復習:第2章第10節(人教AB通用)(解析版)
題型:選擇題
已知f(x)=2x3-6x2+m(m為常數)在[-2,2]上有最大值3,那么此函數在[-2,2]上的最小值是( )
A.-37
B.-29
C.-5
D.以上都不對
查看答案和解析>>
科目:
來源:2011年《龍門亮劍》高三數學(理科)一輪復習:第2章第10節(人教AB通用)(解析版)
題型:選擇題
若函數f(x)=x3-3x+a有3個不同的零點,則實數a的取值范圍是( )
A.(-2,2)
B.[-2,2]
C.(-∞,-1)
D.(1,+∞)
查看答案和解析>>
科目:
來源:2011年《龍門亮劍》高三數學(理科)一輪復習:第2章第10節(人教AB通用)(解析版)
題型:選擇題
設f(x)、g(x)是R上的可導函數,f′(x),g′(x)分別為f(x)、g(x)的導函數,且滿足f′(x)g(x)+f(x)g′(x)<0,則當a<x<b時,有( )
A.f(x)g(b)>f(b)g(x)
B.f(x)g(a)>f(a)g(x)
C.f(x)g(x)>f(b)g(b)
D.f(x)g(x)>f(b)g(a)
查看答案和解析>>
科目:
來源:2011年《龍門亮劍》高三數學(理科)一輪復習:第2章第10節(人教AB通用)(解析版)
題型:選擇題
已知函數f(x)滿足f(x)=f(π-x),且當x∈(-
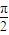
,

)時,f(x)=x+sinx,則( )
A.f(1)<f(2)<f(3)
B.f(2)<f(3)<f(1)
C.f(3)<f(2)<f(1)
D.f(3)<f(1)<f(2)
查看答案和解析>>
科目:
來源:2011年《龍門亮劍》高三數學(理科)一輪復習:第2章第10節(人教AB通用)(解析版)
題型:解答題
已知函數f(x)=alnx+x在區間[2,3]上單調遞增,則實數a的取值范圍是 .
查看答案和解析>>
科目:
來源:2011年《龍門亮劍》高三數學(理科)一輪復習:第2章第10節(人教AB通用)(解析版)
題型:解答題
給出定義:若函數f(x)在D上可導,即f′(x)存在,且導函數f′(x)在D上也可導,則稱f(x)在D上存在二階導函數,記f′(x)=(f′(x))′.若f″(x)<0在D上恒成立,則稱f(x)在D上為凸函數.以下四個函數在(0,

)上不是凸函數的是
.(把你認為正確的序號都填上)
①f(x)=sin x+cos x;
②f(x)=ln x-2x;
③f(x)=-x
3+2x-1;
④f(x)=xe
x.
查看答案和解析>>
科目:
來源:2011年《龍門亮劍》高三數學(理科)一輪復習:第2章第10節(人教AB通用)(解析版)
題型:解答題
將長為52 cm的鐵絲剪成2段,各圍成一個長與寬之比為2:1及3:2的矩形,那么面積之和的最小值為 .
查看答案和解析>>
科目:
來源:2011年《龍門亮劍》高三數學(理科)一輪復習:第2章第10節(人教AB通用)(解析版)
題型:解答題
甲乙兩地相距400千米,汽車從甲地勻速行駛到乙地,速度不得超過100千米/小時,已知該汽車每小時的運輸成本P(元)關于速度v(千米/小時)的函數關系是P=
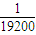
v
4-
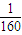
v
3+15v,
(1)求全程運輸成本Q(元)關于速度v的函數關系式;
(2)為使全程運輸成本最少,汽車應以多少速度行駛?并求此時運輸成本的最小值.
查看答案和解析>>

 函數f(x)的定義域為開區間(a,b),導函數f′(x)在(a,b)內的圖象如圖所示,則函數f(x)在開區間(a,b)內有極小值點的個數為( )
函數f(x)的定義域為開區間(a,b),導函數f′(x)在(a,b)內的圖象如圖所示,則函數f(x)在開區間(a,b)內有極小值點的個數為( )

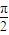 ,
, )時,f(x)=x+sinx,則( )
)時,f(x)=x+sinx,則( ) )上不是凸函數的是 .(把你認為正確的序號都填上)
)上不是凸函數的是 .(把你認為正確的序號都填上)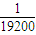 v4-
v4-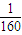 v3+15v,
v3+15v,