
【題目】已知函數f(x)=e﹣x(lnx﹣2k)(k為常數,e=2.71828…是自然對數的底數),曲線y=f(x)在點(1,f(1))處的切線與y軸垂直.
(1)求f(x)的單調區間;
(2)設 ![]() ,對任意x>0,證明:(x+1)g(x)<ex+ex﹣2 .
,對任意x>0,證明:(x+1)g(x)<ex+ex﹣2 .
【答案】
(1)解:因為 ![]() ,
,
由已知得 ![]() ,∴
,∴ ![]() .
.
所以 ![]() ,
,
設 ![]() ,則
,則 ![]() ,
,
在(0,+∞)上恒成立,即k(x)在(0,+∞)上是減函數,
由k(1)=0知,當0<x<1時k(x)>0,
從而f'(x)>0,當x>1時k(x)<0,從而f'(x)<0.
綜上可知,f(x)的單調遞增區間是(0,1),單調遞減區間是(1,+∞)
(2)解:因為x>0,要證原式成立即證 ![]() 成立,
成立,
現證明:對任意x>0,g(x)<1+e﹣2恒成立,
當x≥1時,由(1)知g(x)≤0<1+e﹣2成立;
當0<x<1時,ex>1,且由(1)知g(x)>0,
∴ ![]() .
.
設F(x)=1﹣xlnx﹣x,x∈(0,1),則F'(x)=﹣(lnx+2),
當x∈(0,e﹣2)時,F′(x)>0,
當x∈(e﹣2,1)時,F′(x)<0,
所以當x=e﹣2時,F(x)取得最大值F(e﹣2)=1+e﹣2.
所以g(x)<F(x)≤1+e﹣2,即0<x<1時,g(x)<1+e﹣2.
綜上所述,對任意x>0,g(x)<1+e﹣2.①
令G(x)=ex﹣x﹣1(x>0),則G'(x)=ex﹣1>0恒成立,
所以G(x)在(0,+∞)上遞增,G(x)>G(0)=0恒成立,
即ex>x+1>0,即 ![]() .②
.②
當x≥1時,有: ![]() ;
;
當0<x<1時,由①②式, ![]() ,
,
綜上所述,x>0時, ![]() 成立,
成立,
故原不等式成立
【解析】(1)求出f(x)的導數,通過解關于導函數的不等式,求出函數的單調區間即可;(2)問題轉化為證 ![]() 成立,從而證明
成立,從而證明 ![]() ,設F(x)=1﹣xlnx﹣x,根據函數的單調性證明即可.
,設F(x)=1﹣xlnx﹣x,根據函數的單調性證明即可.
【考點精析】通過靈活運用利用導數研究函數的單調性,掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減即可以解答此題.
在這個區間單調遞減即可以解答此題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】函數是數學中重要的概念之一,同學們在初三、高一分別學習過,也知曉其發展過程.1692年,德國數學家萊布尼茨首次使用function這個詞,1734年瑞士數學家歐拉首次使用符號f(x)表示函數.1859年我國清代數學家李善蘭將function譯作函數,“函”意味著信件,巧妙地揭示了對應關系.密碼學中的加密和解密其實就是函數與反函數.對自變量恰當地賦值是處理函數問題,尤其是處理抽象函數問題的常用方法之一.請你解答下列問題.
已知函數f(x)滿足:對任意的整數a,b均有f(a+b)=f(a) +f(b)+ab+2,且f(-2)=-3.求f(96)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求函數![]() 的最小正周期與單調遞減區間;
的最小正周期與單調遞減區間;
(2)若函數![]() 的圖象上的所有點的橫坐標伸長到原來的
的圖象上的所有點的橫坐標伸長到原來的![]() 倍,所得的圖象與直線
倍,所得的圖象與直線![]() 交點的橫坐標由小到大依次是
交點的橫坐標由小到大依次是![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C的極坐標方程是ρ=2cosθ,以極點為平面直角坐標系的原點,極軸為x軸的正半軸,建立平面直角坐標系,直線L的參數方程是  (t為參數).
(t為參數).
(1)求曲線C的直角坐標方程和直線L的普通方程;
(2)設點P(m,0),若直線L與曲線C交于A,B兩點,且|PA||PB|=1,求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , 常數λ>0,且λa1an=S1+Sn對一切正整數n都成立.
(1)求數列{an}的通項公式;
(2)設a1>0,λ=100,當n為何值時,數列 ![]() 的前n項和最大?
的前n項和最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖給出了一個程序框圖,其作用是輸入x的值,輸出相應的y值.若要使輸入的x值與輸出的y值相等,則這樣的x值有( ) 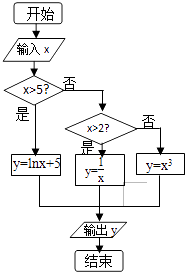
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,![]() 為平行四邊形ABCD所在平面外一點,M,N分別為AB,PC的中點,平面PAD
為平行四邊形ABCD所在平面外一點,M,N分別為AB,PC的中點,平面PAD![]() 平面PBC=
平面PBC=![]() .
.
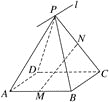
(1)求證:BC∥![]() ;
;
(2)MN與平面PAD是否平行?試證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的前n項和為Sn , a1=a.當n≥2時,Sn2=3n2an+Sn﹣12 , an≠0,n∈N* .
(1)求a的值;
(2)設數列{cn}的前n項和為Tn , 且cn=3n﹣1+a5 , 求使不等式4Tn>Sn成立的最小正整數n的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com