
【題目】設![]() ,
,![]() ,以
,以![]() 表示不是
表示不是![]() 的因數的最小自然數,例如
的因數的最小自然數,例如![]() .若
.若![]() ,又可作
,又可作![]() 等等.如果
等等.如果![]() ,那么
,那么![]() 叫做
叫做![]() 的長度.對一切
的長度.對一切![]() ,
,![]() ,用列舉法表示
,用列舉法表示![]() 的長度構成的集合是______.
的長度構成的集合是______.
【答案】![]()
【解析】
記![]() 的長度為Ln.
的長度為Ln.
很明顯,若奇數n≥3,那么f(n)=2,因此只須討論n為偶數的情況,
我們首先證明,對任何n≥3,f(n)=ps,這里P是素數,s為正整數.
假若不然,若f(n)有兩個不同的素因子,這時總可以將f(n)表為f(n)=ab,其中a、b是大于1的互素的正整數.
由f的定義知,a與b都應能整除n,因(a,b)=1,故ab也應整除n,這與f(n)=ab矛盾.
所以f(n)=ps.
由此可以得出以下結論:
(1)當n為大于1的奇數時,f(n)=2,故Ln=1;
(2)設n為大于2的偶數,如果f(n)=奇數,那么f(f(n))=2,這時Ln=2;
如果f(n)=2s,其中自然數s≥2,那么f(f(n))=f(2s)=3,從而f(f(f(n)))=f(3)=2,這時Ln=3.
綜上可得,用列舉法表示![]() 的長度構成的集合是
的長度構成的集合是![]() .
.


 單元期中期末卷系列答案
單元期中期末卷系列答案科目:高中數學 來源: 題型:
【題目】出租車幾何學是由十九世紀的赫爾曼·閔可夫斯基所創立的。在出租車幾何學中,點還是形如![]() 的有序實數對,直線還是滿足
的有序實數對,直線還是滿足![]() 的所有
的所有![]() 組成的圖形,角度大小的定義也和原來一樣,直角坐標系內任意兩點
組成的圖形,角度大小的定義也和原來一樣,直角坐標系內任意兩點![]() 定義它們之間的一種“距離”:
定義它們之間的一種“距離”:![]() ,請解決以下問題:
,請解決以下問題:
(1)求線段![]() 上一點
上一點![]() 到點
到點![]() 的“距離”;
的“距離”;
(2)定義:“圓”是所有到定點“距離”為定值的點組成的圖形,求“圓”上的所有點到點![]() 的“距離”均為
的“距離”均為![]() 的“圓”方程,并求該“圓”圍成的圖形的面積;
的“圓”方程,并求該“圓”圍成的圖形的面積;
(3)若點![]() 到點
到點![]() 的“距離”和點
的“距離”和點![]() 到點
到點![]() 的“距離”相等,其中實數
的“距離”相等,其中實數![]() 滿足
滿足![]() ,求所有滿足條件的點
,求所有滿足條件的點![]() 的軌跡的長之和.
的軌跡的長之和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知點![]() 是拋物線
是拋物線![]() 上一定點,直線
上一定點,直線![]() 的傾斜角互補,且與拋物線另交于
的傾斜角互補,且與拋物線另交于![]() ,
,![]() 兩個不同的點.
兩個不同的點.
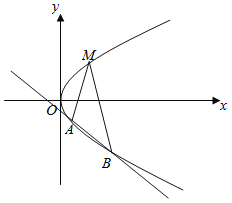
(1)求點![]() 到其準線的距離;
到其準線的距離;
(2)求證:直線![]() 的斜率為定值.
的斜率為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過點A(0,1)且斜率為k的直線l與圓C:(x-2)2+(y-3)2=1交于M,N兩點.
(1)求k的取值范圍;
(2)若![]() =12,其中O為坐標原點,求|MN|.
=12,其中O為坐標原點,求|MN|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,
, ![]() ,離心率為
,離心率為![]() ,
, ![]() 是橢圓
是橢圓![]() 上的動點,當
上的動點,當![]() 時,
時, ![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若過點![]() 的直線交橢圓
的直線交橢圓![]() 于
于![]() ,
, ![]() 兩點,求
兩點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖甲所示,![]() 是梯形
是梯形![]() 的高,
的高,![]() ,
,![]() ,
,![]() ,先將梯形
,先將梯形![]() 沿
沿![]() 折起如圖乙所示的四棱錐
折起如圖乙所示的四棱錐![]() ,使得
,使得![]() .
.
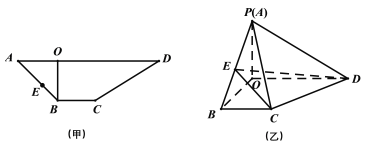
(1)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,請求出
?若存在,請求出![]() 的值,若不存在,請說明理由;
的值,若不存在,請說明理由;
(2)點![]() 是線段
是線段![]() 上一動點,當直線
上一動點,當直線![]() 與
與![]() 所成的角最小時,求二面角
所成的角最小時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一片森林原面積為![]() ,計劃從某年開始,每年砍伐一些樹林,且每年砍伐面積與上一年剩余面積的百分比相等.并計劃砍伐到原面積的一半時,所用時間是10年.為保護生態環境,森林面積至少要保留原面積的
,計劃從某年開始,每年砍伐一些樹林,且每年砍伐面積與上一年剩余面積的百分比相等.并計劃砍伐到原面積的一半時,所用時間是10年.為保護生態環境,森林面積至少要保留原面積的![]() .已知到今年為止,森林剩余面積為原面積的
.已知到今年為止,森林剩余面積為原面積的![]() .
.
(1)求每年砍伐面積與上一年剩余面積的百分比;
(2)到今年為止,該森林已砍伐了多少年?
(3)為保護生態環境,今后最多還能砍伐多少年?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com