

圖7
活動:教師可引導學生思考探究,上例利用向量的幾何法簡捷地解決了平面幾何問題.可否利用向量的坐標運算呢?這需要建立平面直角坐標系,找出所需點的坐標.如果能比較方便地建立起平面直角坐標系,如本例中圖形,很方便建立平面直角坐標系,且圖形中的各個點的坐標也容易寫出,是否利用向量的坐標運算能更快捷地解決問題呢?教師引導學生建系、找點的坐標,然后讓學生獨立完成.
解:建立如圖7所示的平面直角坐標系,取A(0,a),C(c,0),則B(-c,0),
![]() =(0,a),
=(0,a),![]() =(c,a),
=(c,a),![]() =(c,0),
=(c,0),![]() =(2c,0).
=(2c,0).
因為BB′、CC′都是中線,所以![]() =
=![]() (
(![]() +
+![]() )=
)=![]() [(2c,0)+(c,a)]=(
[(2c,0)+(c,a)]=(![]() ).
).
同理,![]() =(-
=(-![]() ).
).
因為BB′⊥CC′,所以-![]() =0,a2=9c2.
=0,a2=9c2.
所以cosA=![]() .
.
點評:比較是最好的學習方法.本例利用的方法與例題1有所不同,但其本質是一致的,教學中引導學生仔細體會這一點,比較兩例的異同,找出其內在的聯系,以達到融會貫通、靈活運用之功效.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數學 來源:學習周報 數學 人教課標高一版(A必修1) 2009-2010學年 第2期 總158期 人教課標高一版 題型:044
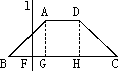
如圖,已知底角為45°的等腰梯形ABCD,底邊BC長為7 cm,腰長為2![]() cm,當一條垂直于底邊BC(垂足為F)的直線l從左至右移動(與梯形ABCD有兩個公共點)時,直線l把梯形分成兩部分,令BF=x,試寫出梯形在直線l左邊部分的面積y關于x的函數解析式.
cm,當一條垂直于底邊BC(垂足為F)的直線l從左至右移動(與梯形ABCD有兩個公共點)時,直線l把梯形分成兩部分,令BF=x,試寫出梯形在直線l左邊部分的面積y關于x的函數解析式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com