
已知點![]() ,一動圓過點
,一動圓過點![]() 且與圓
且與圓![]() 內(nèi)切.
內(nèi)切.
(Ⅰ)求動圓圓心的軌跡![]() 的方程;
的方程;
(Ⅱ)設(shè)點![]() ,點
,點![]() 為曲線
為曲線![]() 上任一點,求點
上任一點,求點![]() 到點
到點![]() 距離的最大值
距離的最大值![]() ;
;
(Ⅲ)在(Ⅱ)的條件下,若![]() ,△
,△![]() 的面積為
的面積為![]() (
(![]() 是坐標(biāo)原點,
是坐標(biāo)原點,![]() 是曲線
是曲線![]() 上橫坐標(biāo)為
上橫坐標(biāo)為![]() 的點),以
的點),以![]() 為邊長的正方形的面積為
為邊長的正方形的面積為![]() .若正數(shù)
.若正數(shù)![]() 滿足
滿足![]() ,問
,問![]() 是否存在最小值,若存在,請求出此最小值,若不存在,請說明理由.
是否存在最小值,若存在,請求出此最小值,若不存在,請說明理由.
解:(Ⅰ)設(shè)圓心坐標(biāo)為![]() ,則動圓的半徑為
,則動圓的半徑為![]() ,
,
又動圓與![]() 內(nèi)切,所以有
內(nèi)切,所以有![]() 化簡得
化簡得![]()
所以動圓圓心軌跡C的方程為![]() . ………………………………4分
. ………………………………4分
(Ⅱ)設(shè)![]() ,則
,則![]()
![]() ,令
,令![]() ,
,![]() ,所以,
,所以,
當(dāng)![]() ,即
,即![]() 時
時![]() 在
在![]() 上是減函數(shù),
上是減函數(shù),![]() ;
;
當(dāng)![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上是增函數(shù),在
上是增函數(shù),在![]() 上是減函數(shù),則
上是減函數(shù),則![]() ;
;
當(dāng)![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上是增函數(shù),
上是增函數(shù),![]() .
.
所以, .…………………………………………9分
.…………………………………………9分
(Ⅲ)當(dāng)![]() 時,
時,![]() ,于是
,于是![]() ,
,![]() ,
,
若正數(shù)![]() 滿足條件,則
滿足條件,則![]() ,即
,即![]() ,
,
![]() ,令
,令![]() ,設(shè)
,設(shè)![]() ,則
,則![]() ,
,![]() ,
,
于是 ,
,
所以,當(dāng)![]() ,即
,即![]() 時,
時,![]() ,
,
即![]() ,
,![]() .所以,
.所以,![]() 存在最小值
存在最小值![]() .………………………………15分
.………………………………15分


 發(fā)散思維新課堂系列答案
發(fā)散思維新課堂系列答案科目:高中數(shù)學(xué) 來源:2011年遼寧省營口市高一上學(xué)期期末檢測數(shù)學(xué)試卷 題型:解答題
.(本小題滿分12分)
已知點 ,一動圓過點
,一動圓過點 且與圓
且與圓 內(nèi)切,
內(nèi)切,
(1)求動圓圓心的軌跡 的方程;
的方程;
(2)設(shè)點 ,點
,點 為曲線
為曲線 上任一點,求點
上任一點,求點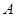 到點
到點 距離的最大值
距離的最大值 ;
;
(3)在 的條件下,設(shè)△
的條件下,設(shè)△ 的面積為
的面積為 (
( 是坐標(biāo)原點,
是坐標(biāo)原點, 是曲線
是曲線 上橫坐標(biāo)為
上橫坐標(biāo)為 的點),以
的點),以 為邊長的正方形的面積為
為邊長的正方形的面積為 .若正數(shù)
.若正數(shù) 滿足
滿足 ,問
,問 是否存在最小值,若存在,請求出此最小值,若不存在,請說明理由.
是否存在最小值,若存在,請求出此最小值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年河北省高三第一次調(diào)研考試數(shù)學(xué)理卷 題型:解答題
((本小題滿分12分)
已知點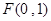 ,一動圓過點
,一動圓過點 且與圓
且與圓 內(nèi)切.
內(nèi)切.
(1)求動圓圓心的軌跡 的方程;
的方程;
(2)設(shè)點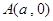 ,點
,點 為曲線
為曲線 上任一點,求點
上任一點,求點 到點
到點 距離的最大值
距離的最大值 ;
;
(3)在 的條件下,設(shè)△
的條件下,設(shè)△ 的面積為
的面積為 (
( 是坐標(biāo)原點,
是坐標(biāo)原點, 是曲線
是曲線 上橫坐標(biāo)為
上橫坐標(biāo)為 的點),以
的點),以 為邊長的正方形的面積為
為邊長的正方形的面積為 .若正數(shù)
.若正數(shù) 使得
使得 恒成立,問
恒成立,問 是否存在最小值,若存在,請求出此最小值,若不存在,請說明理由.
是否存在最小值,若存在,請求出此最小值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年湖北省高二期中考試?yán)砜茢?shù)學(xué)試卷 題型:解答題
(本小題滿分15分)已知點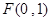 ,一動圓過點
,一動圓過點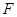 且與圓
且與圓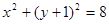 內(nèi)切.
內(nèi)切.
(Ⅰ)求動圓圓心的軌跡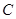 的方程;
的方程;
(Ⅱ)設(shè)點 ,點
,點 為曲線
為曲線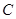 上任一點,求點
上任一點,求點 到點
到點 距離的最大值
距離的最大值 ;
;
(Ⅲ)在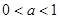 的條件下,設(shè)△
的條件下,設(shè)△ 的面積為
的面積為 (
( 是坐標(biāo)原點,
是坐標(biāo)原點, 是曲線
是曲線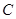 上橫坐標(biāo)為
上橫坐標(biāo)為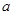 的點),以
的點),以 為邊長的正方形的面積為
為邊長的正方形的面積為 .若正數(shù)
.若正數(shù) 滿足
滿足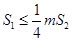 ,問
,問 是否存在最小值,若存在,請求出此最小值,若不存在,請說明理由.
是否存在最小值,若存在,請求出此最小值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年湖北省高二期中考試文科數(shù)學(xué)試卷 題型:解答題
(本小題滿分13分)已知點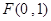 ,一動圓過點
,一動圓過點 且與圓
且與圓 內(nèi)切.
內(nèi)切.
(Ⅰ)求動圓圓心的軌跡 的方程;
的方程;
(Ⅱ)設(shè)點 ,點
,點 為曲線
為曲線 上任一點,求點
上任一點,求點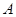 到點
到點 距離的最大值
距離的最大值 (用
(用 表示);
表示);
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
已知點![]() ,一動圓過點
,一動圓過點![]() 且與圓
且與圓![]() 內(nèi)切.
內(nèi)切.
(Ⅰ)求動圓圓心的軌跡![]() 的方程;
的方程;
(Ⅱ)設(shè)點![]() ,點
,點![]() 為曲線
為曲線![]() 上任一點,求點
上任一點,求點![]() 到點
到點![]() 距離的最大值
距離的最大值![]() (用
(用![]() 表示);
表示);
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com