
解:(1)定義域為(0,+∞),
由f ′(x)=exlnx(lnx+1),
令f ′(x)>0,解得x>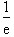 ;令f '(x)<0,解得0<x<
;令f '(x)<0,解得0<x<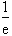 .
.
故f(x)的增區間:(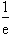 ,+∞),減區間:(0,
,+∞),減區間:(0, ),
),
(2)即證:(x+1)ln(x+1)>2x-1 ln(x+1)>
ln(x+1)>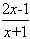
 ln(x+1)-
ln(x+1)-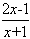 >0
>0
令g(x)=ln(x+1)- ,由g'(x)=
,由g'(x)= ,
,
令g′(x)=0,得x=2,且g(x)在(0,2)↓,在(2,+∞)↑,所以g(x)min=g(2)=ln3﹣1,
故當x>0時,有g(x)≥g(2)=ln3﹣1>0得證。
(3)由(2)得ln(x+1)>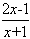 ,即ln(x+1)>2-
,即ln(x+1)>2-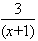 ,
,
所以ln[k(k+1)+1]>2-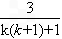 >2-
>2- ,
,
則:ln(1×2+1)+ln(2×3+1)+…+ln[(n(n+1)]+1>(2- )+(2-
)+(2- )+...+[2-
)+...+[2- ]=2n-3+
]=2n-3+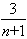 >2n-3。.
>2n-3。.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com