
【題目】已知函數(shù)![]() .
.
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)設(shè)![]() ,當(dāng)
,當(dāng)![]() 時,對任意
時,對任意![]() ,存在
,存在![]() ,使
,使![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析.
(2)![]() .
.
【解析】分析:(1)先求一階導(dǎo)函數(shù)![]() 的根,求解
的根,求解![]() 或
或![]() 的解集,寫出單調(diào)區(qū)間。
的解集,寫出單調(diào)區(qū)間。
(2)當(dāng)![]() 時,求出
時,求出![]() 的最小值,存在
的最小值,存在![]() ,使
,使![]() 的最小值,
的最小值,
再分離變量構(gòu)建函數(shù)![]() ,解
,解![]() 。
。
詳解:(1)![]() 的定義域?yàn)?/span>
的定義域?yàn)?/span>![]() ,
,
又![]() ,
,
令![]() ,得
,得![]() 或
或![]() .
.
當(dāng)![]() ,則
,則![]() ,由
,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
函數(shù)![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增.
上單調(diào)遞增.
當(dāng)![]() ,則
,則![]() ,由
,由![]() 得
得![]() ,
,
由![]() 得
得![]() 或
或![]() ,
,
函數(shù)![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 和
和![]() 上單調(diào)遞增.
上單調(diào)遞增.
當(dāng)![]() ,則
,則![]() ,可得
,可得![]() ,
,
此時函數(shù)![]() 在
在![]() 上單調(diào)遞增.
上單調(diào)遞增.
當(dāng)![]() 時,則
時,則![]() ,由
,由![]() 得
得![]() ,
,
由![]() 得
得![]() 或
或![]() ,
,
函數(shù)![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 和
和![]() 上單調(diào)遞增.
上單調(diào)遞增.
(2)當(dāng)![]() 時,由(1)得函數(shù)
時,由(1)得函數(shù)![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
在![]() 和
和![]() 上單調(diào)遞增,
上單調(diào)遞增,
從而![]() 在
在![]() 上的最小值為
上的最小值為![]() .
.
對任意![]() ,存在
,存在![]() ,使
,使![]() ,
,
即存在![]() ,
,![]() 函數(shù)值不超過
函數(shù)值不超過![]() 在區(qū)間
在區(qū)間![]() 上的最小值
上的最小值![]() .
.
由![]() 得
得![]() ,
,![]() .
.
記![]() ,則當(dāng)
,則當(dāng)![]() 時,
時,![]() .
.
![]()
![]() ,當(dāng)
,當(dāng)![]() ,顯然有
,顯然有![]() ,
,
當(dāng)![]() ,
,![]() ,
,
故![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減,得
上單調(diào)遞減,得![]() ,
,
從而![]() 的取值范圍為
的取值范圍為![]() .
.


 黃岡小狀元解決問題天天練系列答案
黃岡小狀元解決問題天天練系列答案 三點(diǎn)一測快樂周計劃系列答案
三點(diǎn)一測快樂周計劃系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知曲線![]() 的參數(shù)方程為:
的參數(shù)方程為:![]() (
(![]() 為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),
為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,直線
,直線![]() 的直角坐標(biāo)方程為
的直角坐標(biāo)方程為![]() .
.
(l)求曲線![]() 和直線
和直線![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)已知直線![]() 分別與曲線
分別與曲線![]() 、曲線
、曲線![]() 交異于極點(diǎn)的
交異于極點(diǎn)的![]() ,若
,若![]() 的極徑分別為
的極徑分別為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 、
、![]() 、
、![]() 表示不同的直線,
表示不同的直線,![]() 、
、![]() 、
、![]() 表示不同的平面,給出下列
表示不同的平面,給出下列![]() 個命題:其中命題正確的個數(shù)是( )
個命題:其中命題正確的個數(shù)是( )
①若![]() ,且
,且![]() ,則
,則![]() ;
;
②若![]() ,且
,且![]() ,則
,則![]() ;
;
③若![]() ,
,![]() ,
,![]() ,則
,則![]() ;
;
④ 若![]() ,
,![]() ,
,![]() ,且
,且![]() ,則
,則![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,PD⊥底面ABCD,底面ABCD是邊長為a的正方形,且PD=a.
(1)求四棱錐P﹣ABCD的體積;
(2)若E為PC中點(diǎn),求證:PA∥平面BDE;
(3)求直線PB與平面ABCD所成角的正切值.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市政府為了節(jié)約生活用電,計劃在本市試行居民生活用電定額管理,即確定一戶居民月用電量標(biāo)準(zhǔn)a,用電量不超過a的部分按平價收費(fèi),超出a的部分按議價收費(fèi)![]() 為此,政府調(diào)查了100戶居民的月平均用電量
為此,政府調(diào)查了100戶居民的月平均用電量![]() 單位:度
單位:度![]() ,以
,以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分組的頻率分布直方圖如圖所示.
分組的頻率分布直方圖如圖所示.
![]() 根據(jù)頻率分布直方圖的數(shù)據(jù),求直方圖中x的值并估計該市每戶居民月平均用電量
根據(jù)頻率分布直方圖的數(shù)據(jù),求直方圖中x的值并估計該市每戶居民月平均用電量![]() 的值;
的值;
![]() 用頻率估計概率,利用
用頻率估計概率,利用![]() 的結(jié)果,假設(shè)該市每戶居民月平均用電量X服從正態(tài)分布
的結(jié)果,假設(shè)該市每戶居民月平均用電量X服從正態(tài)分布![]()
![]() 估計該市居民月平均用電量介于
估計該市居民月平均用電量介于![]() 度之間的概率;
度之間的概率;
![]() 利用
利用![]() 的結(jié)論,從該市所有居民中隨機(jī)抽取3戶,記月平均用電量介于
的結(jié)論,從該市所有居民中隨機(jī)抽取3戶,記月平均用電量介于![]() 度之間的戶數(shù)為
度之間的戶數(shù)為![]() ,求
,求![]() 的分布列及數(shù)學(xué)期望
的分布列及數(shù)學(xué)期望![]() .
.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地區(qū)某長產(chǎn)品近幾年的產(chǎn)量統(tǒng)計如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代碼 | 1 | 2 | 3 | 4 | 5 | 6 |
年產(chǎn)量 | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根據(jù)表中數(shù)據(jù),建立![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若近幾年該農(nóng)產(chǎn)品每千克的價格![]() (單位:元)與年產(chǎn)量
(單位:元)與年產(chǎn)量![]() 滿足的函數(shù)關(guān)系式為
滿足的函數(shù)關(guān)系式為![]() ,且每年該農(nóng)產(chǎn)品都能售完.
,且每年該農(nóng)產(chǎn)品都能售完.
①根據(jù)(1)中所建立的回歸方程預(yù)測該地區(qū)2018(![]() )年該農(nóng)產(chǎn)品的產(chǎn)量;
)年該農(nóng)產(chǎn)品的產(chǎn)量;
②當(dāng)![]() (
(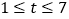 )為何值時,銷售額
)為何值時,銷售額![]() 最大?
最大?
附:對于一組數(shù)據(jù)![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: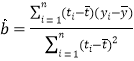 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】秸稈還田是當(dāng)今世界上普通重視的一項(xiàng)培肥地力的增產(chǎn)措施,在杜絕了秸稈焚燒所造成的大氣污染的同時還有增肥增產(chǎn)作用.某農(nóng)機(jī)戶為了達(dá)到在收割的同時讓秸稈還田,花![]() 元購買了一臺新型聯(lián)合收割機(jī),每年用于收割可以收入
元購買了一臺新型聯(lián)合收割機(jī),每年用于收割可以收入![]() 萬元(已減去所用柴油費(fèi));該收割機(jī)每年都要定期進(jìn)行維修保養(yǎng),第一年由廠方免費(fèi)維修保養(yǎng),第二年及以后由該農(nóng)機(jī)戶付費(fèi)維修保養(yǎng),所付費(fèi)用
萬元(已減去所用柴油費(fèi));該收割機(jī)每年都要定期進(jìn)行維修保養(yǎng),第一年由廠方免費(fèi)維修保養(yǎng),第二年及以后由該農(nóng)機(jī)戶付費(fèi)維修保養(yǎng),所付費(fèi)用![]() (元)與使用年數(shù)
(元)與使用年數(shù)![]() 的關(guān)系為:
的關(guān)系為:![]() ,已知第二年付費(fèi)
,已知第二年付費(fèi)![]() 元,第五年付費(fèi)
元,第五年付費(fèi)![]() 元.
元.
(1)試求出該農(nóng)機(jī)戶用于維修保養(yǎng)的費(fèi)用![]() (元)與使用年數(shù)
(元)與使用年數(shù)![]() 的函數(shù)關(guān)系;
的函數(shù)關(guān)系;
(2)這臺收割機(jī)使用多少年,可使平均收益最大?(收益=收入-維修保養(yǎng)費(fèi)用-購買機(jī)械費(fèi)用)
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com