
【題目】已知f(x)是定義在[﹣1,1]上的奇函數,且f(1)=1,若a,b∈[﹣1,1],a+b≠0時,有 ![]() >0成立. (Ⅰ)判斷f(x)在[﹣1,1]上的單調性,并證明;
>0成立. (Ⅰ)判斷f(x)在[﹣1,1]上的單調性,并證明;
(Ⅱ)解不等式:f(2x﹣1)<f(1﹣3x);
(Ⅲ)若f(x)≤m2﹣2am+1對所有的a∈[﹣1,1]恒成立,求實數m的取值范圍.
【答案】解:(Ⅰ)任取x1 , x2∈[﹣1,1],且x1<x2 , 則﹣x2∈[﹣1,1],∵f(x)為奇函數, ∴f(x1)﹣f(x2)=f(x1)+f(﹣x2)= ![]() (x1﹣x2),…(2分)
(x1﹣x2),…(2分)
由已知得 ![]() >0,x1﹣x2<0,∴f(x1)﹣f(x2)<0,即f(x1)<f(x2).
>0,x1﹣x2<0,∴f(x1)﹣f(x2)<0,即f(x1)<f(x2).
∴f(x)在[﹣1,1]上單調遞增.
(Ⅱ)∵f(x)在[﹣1,1]上單調遞增,∴ 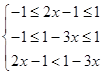
∴不等式的解集為 ![]() .
.
(Ⅲ)∵f(1)=1,f(x)在[﹣1,1]上單調遞增.∴在[﹣1,1]上,f(x)≤1.
問題轉化為m2﹣2am+1≥1,即m2﹣2am≥0,對a∈[﹣1,1]恒成立.
下面來求m的取值范圍.設g(a)=﹣2ma+m2≥0.
①若m=0,則g(a)=0≥0,對a∈[﹣1,1]恒成立.
②若m≠0,則g(a)為a的一次函數,若g(a)≥0,對a∈[﹣1,1]恒成立,
必須g(﹣1)≥0且g(1)≥0,∴m≤﹣2或m≥2.
綜上,m=0 或m≤﹣2或m≥2
【解析】(Ⅰ)任取x1 , x2∈[﹣1,1],且x1<x2 , 利用函數的單調性的定義證明f(x)在[﹣1,1]上單調遞增.(Ⅱ)利用f(x)在[﹣1,1]上單調遞增,列出不等式組,即可求出不等式的解集.(Ⅲ)問題轉化為m2﹣2am≥0,對a∈[﹣1,1]恒成立,通過①若m=0,②若m≠0,分類討論,判斷求解即可.


科目:高中數學 來源: 題型:
【題目】某班有36名同學參加數學、物理、化學課外探究小組,每名同學至多參加兩個小組,已知參加數學、物理、化學小組的人數分別為26,15,13,同時參加數學和物理小組的有6人,同時參加物理和化學小組的有4人,則同時參加數學和化學小組的有人.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|x=a0+a1×2+a2×22+a3×23},其中ai∈{0,1,2}(i=0,1,2,3),且a0≠0,則A中所有元素之和等于 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設小明家訂了一份報紙,送報人可能在早上6:30﹣7:30之間把報紙送到小明家,小明父親離開家去工作的時間在早上7:00﹣8:00之間,問小明父親在離開家前能得到報紙(稱為事件A)的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知,圓C:x2+y2﹣8y+12=0,直線l:ax+y+2a=0.
(1)當a為何值時,直線l與圓C相切;
(2)當直線l與圓C相交于A、B兩點,且AB=2 ![]() 時,求直線l的方程.
時,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若![]() ,求曲線
,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)若函數![]() 在其定義域內為增函數,求
在其定義域內為增函數,求![]() 的取值范圍;
的取值范圍;
(3)在(2)的條件下,設函數![]() ,若在
,若在![]() 上至少存在一點
上至少存在一點![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某機構為調查我國公民對申辦奧運會的態度,選了某小區的100位居民調查結果統計如下:
支持 | 不支持 | 合計 | |
年齡不大于50歲 | 80 | ||
年齡大于50歲 | 10 | ||
合計 | 70 | 100 |
(1)根據已有數據,把表格數據填寫完整;
(2)能否在犯錯誤的概率不超過5%的前提下認為不同年齡與支持申辦奧運無關?
(3)已知在被調查的年齡大于50歲的支持者中有5名女性,其中2位是女教師,現從這5名女性中隨機抽取3人,求至多有1位女教師的概率.
附:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com