
 ),β∈(
),β∈( ,π)且sin(α+β)=
,π)且sin(α+β)= ,cosβ=-
,cosβ=- .求sinα.
.求sinα. ,sinβ=
,sinβ=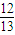 .利用同角三角函數關系求值時要判斷角的終邊所在的象限,來確定三角函數值的符號,此是正確求值的關鍵,由于α=α+β-β,故sinα=sin[(α+β)-β]=sin(α+β)cosβ-cos(α+β)sinβ,將各角的三角函數值代入求sinα.
.利用同角三角函數關系求值時要判斷角的終邊所在的象限,來確定三角函數值的符號,此是正確求值的關鍵,由于α=α+β-β,故sinα=sin[(α+β)-β]=sin(α+β)cosβ-cos(α+β)sinβ,將各角的三角函數值代入求sinα.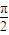 ,π),cosβ=-
,π),cosβ=-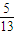 ,∴sinβ=
,∴sinβ= .
. ,
,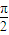 <β<π,
<β<π, <α+β<
<α+β< ,又sin(α+β)=
,又sin(α+β)= ,
,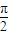 <α+β<π,
<α+β<π,
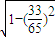 =-
=- ,
,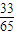 •(-
•(- )-(-
)-(- )•
)•
 .
.

 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源: 題型:
| 1 |
| 8 |
| 2 |
| 3 |
| ln3-ln2 |
| 5 |
| ln2 |
| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com