
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是矩形,側棱
是矩形,側棱![]() 底面
底面![]() ,且
,且![]() ,過棱
,過棱![]() 的中點
的中點![]() ,作
,作![]() 交
交![]() 于點
于點![]() .
.
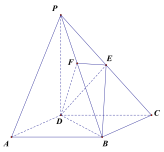
(1)證明:![]() 平面
平面![]() ;
;
(2)若面![]() 與面
與面![]() 所成二面角的大小為
所成二面角的大小為![]() ,求
,求![]() 與面
與面![]() 所成角的正弦值.
所成角的正弦值.
科目:高中數學 來源: 題型:
【題目】如圖,已知![]() 中,
中,![]() ,點
,點![]() 平面
平面![]() ,點
,點![]() 在平面
在平面![]() 的同側,且
的同側,且![]() 在平面
在平面![]() 上的射影分別為
上的射影分別為![]() ,
,![]() .
.
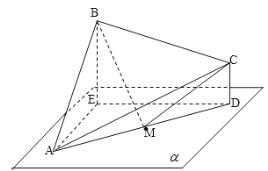
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 是
是![]() 中點,求平面
中點,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 的參數方程是
的參數方程是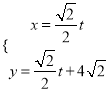 (
(![]() 是參數),以坐標原點為原點,
是參數),以坐標原點為原點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)判斷直線![]() 與曲線
與曲線![]() 的位置關系;
的位置關系;
(2)過直線![]() 上的點作曲線
上的點作曲線![]() 的切線,求切線長的最小值.
的切線,求切線長的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中無理數
,其中無理數![]() .
.
(Ⅰ)若函數![]() 有兩個極值點,求
有兩個極值點,求![]() 的取值范圍;
的取值范圍;
(Ⅱ)若函數![]() 的極值點有三個,最小的記為
的極值點有三個,最小的記為![]() ,最大的記為
,最大的記為![]() ,若
,若![]() 的最大值為
的最大值為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,直線l:![]() ,P為直線l上一點,且點P在極軸上方
,P為直線l上一點,且點P在極軸上方![]() 以OP為一邊作正三角形
以OP為一邊作正三角形![]() 逆時針方向
逆時針方向![]() ,且
,且![]() 面積為
面積為![]() .
.
![]() 求Q點的極坐標;
求Q點的極坐標;
![]() 求
求![]() 外接圓的極坐標方程,并判斷直線l與
外接圓的極坐標方程,并判斷直線l與![]() 外接圓的位置關系.
外接圓的位置關系.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 過點
過點![]() ,過坐標原點
,過坐標原點![]() 作兩條互相垂直的射線與橢圓
作兩條互相垂直的射線與橢圓![]() 分別交于
分別交于![]() ,
,![]() 兩點.
兩點.
(1)證明:當![]() 取得最小值時,橢圓
取得最小值時,橢圓![]() 的離心率為
的離心率為![]() .
.
(2)若橢圓![]() 的焦距為2,是否存在定圓與直線
的焦距為2,是否存在定圓與直線![]() 總相切?若存在,求定圓的方程;若不存在,請說明理由.
總相切?若存在,求定圓的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十九大提出,堅決打贏脫貧攻堅戰,某幫扶單位為幫助定點扶貧村真脫貧,堅持扶貧同扶智相結合,幫助貧困村種植蜜柚,并利用電商進行銷售,為了更好地銷售,現從該村的蜜柚樹上隨機摘下了100個蜜柚進行測重,其質量分別在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (單位:克)中,其頻率分布直方圖如圖所示.
(單位:克)中,其頻率分布直方圖如圖所示.
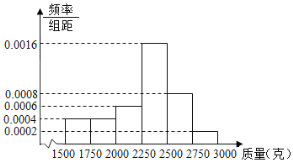
(1)按分層抽樣的方法從質量落在![]() ,
,![]() 的蜜柚中抽取5個,再從這5個蜜柚中隨機抽取2個,求這2個蜜柚質量均小于2000克的概率;
的蜜柚中抽取5個,再從這5個蜜柚中隨機抽取2個,求這2個蜜柚質量均小于2000克的概率;
(2)以各組數據的中間數代表這組數據的平均水平,以頻率代表概率,已知該貧困村的蜜柚樹上大約還有5000個蜜柚等待出售,某電商提出兩種收購方案:
A. 所有蜜柚均以40元/千克收購;
B. 低于2250克的蜜柚以60元/個收購,高于或等于2250克的以80元/個收購.
請你通過計算為該村選擇收益最好的方案.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,以
中,以![]() 為極點,
為極點,![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ;直線
;直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),直線
為參數),直線![]() 與曲線
與曲線![]() 分別交于
分別交于![]() ,
,![]() 兩點.
兩點.
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)若點![]() 的極坐標為
的極坐標為![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex![]() (x﹣a)2+4.
(x﹣a)2+4.
(1)若f(x)在(﹣∞,+∞)上單調遞增,求a的取值范圍;
(2)若x≥0,不等式f(x)≥0恒成立,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com