【題目】已知直線
的參數方程是
（
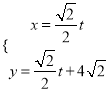是參數），以坐標原點為原點， 
軸的正半軸為極軸建立極坐標系，曲線
的極坐標方程為
.
（1）判斷直線
與曲線
的位置關系；
（2）過直線
上的點作曲線
的切線，求切線長的最小值.
科目：高中數學 來源： 題型：
【題目】甲船在島B的正南A處，AB＝10千米．甲船以每小時4千米的速度向北航行，同時，乙船自B出發(fā)以每小時6千米的速度向北偏東60°的方向駛去．當甲船在A，B之間，且甲、乙兩船相距最近時，它們所航行的時間是( )
A. 
分鐘 B. 
小時 C. 21.5分鐘 D. 2.15分鐘
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對某地區(qū)兒童的身高與體重的一組數據，我們用兩種模型①
，②
擬合，得到回歸方程分別為
， 
，作殘差分析，如表：
身高 | 60 | 70 | 80 | 90 | 100 | 110 |
體重 | 6 | 8 | 10 | 14 | 15 | 18 |
| 0.41 | 0.01 | 1.21 | －0.19 | 0.41 | |
| －0.36 | 0.07 | 0.12 | 1.69 | －0.34 | －1.12 |
（Ⅰ）求表中空格內的值；
（Ⅱ）根據殘差比較模型①，②的擬合效果，決定選擇哪個模型；
（Ⅲ）殘差大于
的樣本點被認為是異常數據，應剔除，剔除后對(Ⅱ)所選擇的模型重新建立回歸方程.
（結果保留到小數點后兩位）
附：對于一組數據
，其回歸直線
的斜率和截距的最小二乘法估計分別為
， 
.
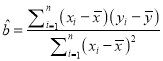查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，正方體
的棱長為
，
，
分別是棱
，
的中點，過直線，的平面分別與棱
、
交于
，
，設
，
，給出以下四個命題：
①平面
平面
；
②當且僅當
時，四邊形
的面積最小；
③四邊形周長
，
是單調函數；
④四棱錐
的體積
為常函數；
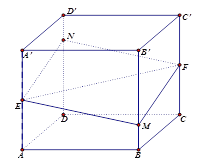
以上命題中假命題的序號為（ ）．
A. ①④ B. ② C. ③ D. ③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
