
分析 (Ⅰ)求出原函數(shù)的導函數(shù),得到f′(π),再求出f(π),代入直線方程的點斜式得答案;
(Ⅱ)求出原函數(shù)的導函數(shù)f′(x)=$\frac{x•cosx-sinx}{{x}^{2}}$,令g(x)=x•cosx-sinx,可得g′(x)<0,得到g(x)在(0,π)上為減函數(shù),又g(x)<g(0)=0.可得f′(x)<0;
(Ⅲ)由(Ⅱ)可知,f(x)在(0,π)上為減函數(shù),得到0<α<$\frac{π}{2}$<β<π時,f(α)>f(β);當π≤β<2π時,f(β)=$\frac{sinβ}{β}$<0,可得f(α)>f(β).
解答 解:(Ⅰ)f′(x)=$\frac{x•cosx-sinx}{{x}^{2}}$,
f′(π)=-$\frac{1}{π}$,而f(π)=0,
∴曲線y=f(x)在點A(π,f(π))處的切線方程為y-0=$-\frac{1}{π}$(x-π),
即x+πy-π=0;
證明:(Ⅱ)f′(x)=$\frac{x•cosx-sinx}{{x}^{2}}$,
令g(x)=x•cosx-sinx,則g′(x)=cosx-x•sinx-cosx=-xsinx<0,
∴g(x)在(0,π)上為減函數(shù),則g(x)<g(0)=0.
∴f′(x)<0;
解:(Ⅲ)若0<α<$\frac{π}{2}$<β<2π,則f(α)>f(β).
事實上,當0<α<$\frac{π}{2}$<β<π時,
由(Ⅱ)知f′(x)<0,
故f(x)在(0,π)上為減函數(shù),
由0<α<$\frac{π}{2}$<β<π,可得f(α)>f(β);
當0<α<$\frac{π}{2}$,π≤β<2π時,f(α)=$\frac{sinα}{α}>0$,f(β)=$\frac{sinβ}{β}$<0,可得f(α)>f(β).
綜上,若0<α<$\frac{π}{2}$<β<2π,則f(α)>f(β).
點評 本題考查利用導數(shù)研究函數(shù)的單調(diào)性,考查利用導數(shù)求過曲線上某點處的切線方程,體現(xiàn)了分類討論的數(shù)學思想方法,是中檔題.


科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
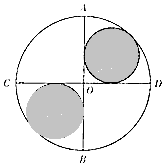 如圖所示,已知AB,CD是圓O中兩條互相垂直的直徑,兩個小圓與圓O以及AB,CD均相切,則往圓O內(nèi)投擲一個點,該點落在陰影部分的概率為( )
如圖所示,已知AB,CD是圓O中兩條互相垂直的直徑,兩個小圓與圓O以及AB,CD均相切,則往圓O內(nèi)投擲一個點,該點落在陰影部分的概率為( )| A. | 12-8$\sqrt{2}$ | B. | 3-2$\sqrt{2}$ | C. | 8-5$\sqrt{2}$ | D. | 6-4$\sqrt{2}$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
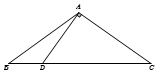 如圖,在△ABC中,已知點D在BC邊上,AD⊥AC,AB=2$\sqrt{5}$,sin∠BAC=$\frac{{\sqrt{5}}}{3}$,AD=3,則BD的長為3.
如圖,在△ABC中,已知點D在BC邊上,AD⊥AC,AB=2$\sqrt{5}$,sin∠BAC=$\frac{{\sqrt{5}}}{3}$,AD=3,則BD的長為3.查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
 如圖,已知雙曲線$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦點分別為F1、F2,|F1F2|=4,P是雙曲線右支上一點,直線PF2交y軸于點A,△APF1的內(nèi)切圓切邊PF1于點Q,若|PQ|=1,則雙曲線的離心率為2.
如圖,已知雙曲線$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦點分別為F1、F2,|F1F2|=4,P是雙曲線右支上一點,直線PF2交y軸于點A,△APF1的內(nèi)切圓切邊PF1于點Q,若|PQ|=1,則雙曲線的離心率為2.查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
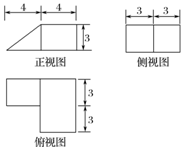
| A. | 72 cm3 | B. | 90 cm3 | C. | 108 cm3 | D. | 138 cm3 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com