
【題目】已知函數![]() .
.
(1)討論![]() 在
在![]() 上的單調性;
上的單調性;
(2)是否存在實數![]() ,使得
,使得![]() 在
在![]() 上的最大值為
上的最大值為![]() ,若存在,求滿足條件的
,若存在,求滿足條件的![]() 的個數;若不存在,請說明理由.
的個數;若不存在,請說明理由.
【答案】(1)見解析;(2)1個
【解析】試題分析:(1)求導數可得![]() ,對a進行分類討論得:①當
,對a進行分類討論得:①當![]() 時,
時, ![]() 在
在![]() 上單調遞增,②當
上單調遞增,②當![]() 或
或![]() 時,
時, ![]() 在
在![]() 上單調遞減,③當
上單調遞減,③當![]() 且
且![]() 時,
時, ![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減。(2)結合(1)可得當
上單調遞減。(2)結合(1)可得當![]() 時,
時, ![]() ,故有
,故有![]() ,即
,即![]() ,可判斷方程
,可判斷方程![]() 只有1個實數解,所以存在滿足條件的實數a,且只有1個。
只有1個實數解,所以存在滿足條件的實數a,且只有1個。
試題解析:
(1)∵![]() ,
,
∴![]() ,
,
①當![]() 時,
時, ![]() 在
在![]() 上單調遞增。
上單調遞增。
②當![]() ,即
,即![]() 或
或![]() 時,
時, ![]() ,
,
∴![]() 在
在![]() 上單調遞減。
上單調遞減。
③當![]() 且
且![]() 時,
時,
由![]() 得
得![]() .
.
令![]() 得
得![]() ;令
;令![]() 得
得![]() .
.
∴![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
綜上,當![]() 時,
時, ![]() 在
在![]() 上遞增;
上遞增;
當![]() 或
或![]() 時,
時, ![]() 在
在![]() 上遞減;
上遞減;
當![]() 且
且![]() 時,
時, ![]() 在
在![]() 上遞增,在
上遞增,在![]() 上遞減.
上遞減.
(2)易知![]() ,由(1)知
,由(1)知![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
∴ 當![]() 時,
時, ![]() 有極大值,也為最大值,且
有極大值,也為最大值,且![]()
由題意得 ![]() ,
,
即![]() ,
,
設![]() ,易知
,易知![]() 為增函數,且
為增函數,且![]() ,
,
∴![]() 的唯一零點在
的唯一零點在![]() 上,
上,
∴ 方程![]() 有唯一解,
有唯一解,
∴ 存在實數![]() 滿足條件,且實數
滿足條件,且實數![]() 的個數為1個.
的個數為1個.


 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案科目:高中數學 來源: 題型:
【題目】已知函數為常數![]()
(1)當![]() 在
在![]() 處取得極值時,若關于x的方程
處取得極值時,若關于x的方程![]() 在
在![]() 上恰有兩個不相等的實數根,求實數b的取值范圍.
上恰有兩個不相等的實數根,求實數b的取值范圍.
(2)若對任意的![]() ,總存在
,總存在![]() ,使不等式
,使不等式![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓M:: ![]() +
+ ![]() =1(a>0)的一個焦點為F(﹣1,0),左右頂點分別為A,B.經過點F的直線l與橢圓M交于C,D兩點.
=1(a>0)的一個焦點為F(﹣1,0),左右頂點分別為A,B.經過點F的直線l與橢圓M交于C,D兩點.
(1)求橢圓方程;
(2)當直線l的傾斜角為45°時,求線段CD的長;
(3)記△ABD與△ABC的面積分別為S1和S2 , 求|S1﹣S2|的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=ax3﹣3x+1 對于x∈[﹣1,1]總有f(x)≥0成立,則a 的取值范圍為( )
A.[2,+∞)
B.[4,+∞)
C.{4}
D.[2,4]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】每年的三月十二日,是中國的植樹節,林管部門在植樹前,為保證樹苗的質量,都會在植樹前對樹苗進行檢測.現從甲、乙兩批樹苗中各抽測了10株樹苗的高度,規定高于128厘米的為“良種樹苗”,測得高度如下(單位:厘米)
甲:137,121,131,120,129,119,132,123,125,133
乙:110,130,147,127,146,114,126,110,144,146
(1)根據抽測結果,完成答題卷中的莖葉圖,并根據你填寫的莖葉圖,對甲、乙兩批樹苗的高度作比較,寫出對兩種樹苗高度的統計結論;
(2)設抽測的10株甲種樹苗高度平均值為 ![]() ,將這10株樹苗的高度依次輸入按程序框圖進行運算,
,將這10株樹苗的高度依次輸入按程序框圖進行運算,
(如圖)問輸出的S大小為多少?并說明S的統計學意義.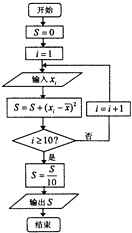
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com