已知函數(shù)

(I)求f(x)在[0,1]上的極值;
(II)若對任意

成立,求實數(shù)a的取值范圍;
(III)若關于x的方程

在[0,1]上恰有兩個不同的實根,求實數(shù)b的取值范圍.
本試題主要是考查了導數(shù)在研究函數(shù)中的運用。
(1)求解定義域和導數(shù),進而利用導數(shù)的符號來判定函數(shù)的單調性,進而得到極值的求解。
(2)由
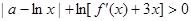
得
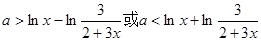
,
依題意知
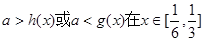
上恒成立
(3)由
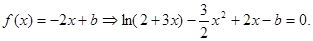
令
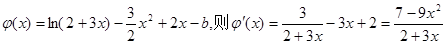
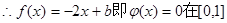
恰有兩個不同實根,得到參數(shù)的范圍。
解:(I)
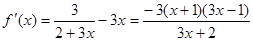
,
令
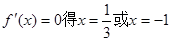
(舍去)
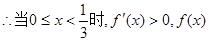
單調遞增;
當
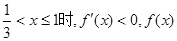
單調遞減.
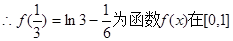
上的極大值
(II)由
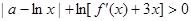
得
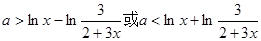
, …………①
設
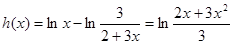
,
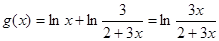
,
依題意知
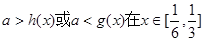
上恒成立,
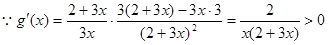
,

,
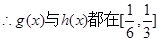
上單增,要使不等式①成立,
當且僅當
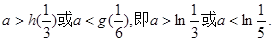
(III)由
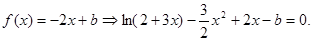
令
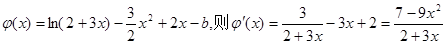
,
當

上遞增;
當
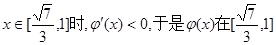
上遞減
而
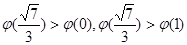
,
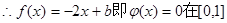
恰有兩個不同實根等價于
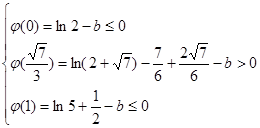
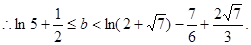
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)f(x)=x

+4x+3,g(x)為一次函數(shù),若f(g(x))=x

+10x+24,求g(x)
的表達式.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
設函數(shù)
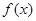
的定義域為
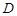
,如果對于任意
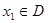
,存在唯一
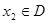
,使
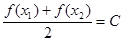
(
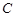
為常數(shù))成立,則稱
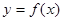
在
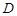
上的均值為
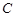
,給出下列四個
函數(shù): ①
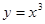
;②
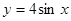
;③
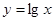
;④
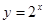
. 則滿足在其定義域上均值為2
的所有函數(shù)是__________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設
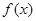
為定義在R上的奇函數(shù),當
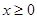
時,
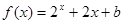
(
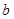
為常數(shù)),則
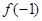
=( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
設函數(shù)
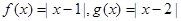
.
(Ⅰ)解不等式
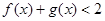
;
(Ⅱ)對于實數(shù)
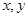
,若

,求證
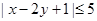
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
函數(shù)
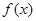
是定義域為

的偶函數(shù),當
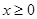
時,

,則當
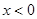
時,
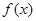
的表達式為___________
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
下列用圖表給出的函數(shù)關系中,當x=6時,對應的函數(shù)值y等于( )
x
| 0<x≤1
| 1<x≤5
| 5<x≤10
| x>10
|
y
| 1
| 2
| 3
| 4
|
A、4 B、3 C、2 D、1
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
設f(x)=
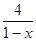
,若f(a)=2,則實數(shù)a=
.
查看答案和解析>>


 成立,求實數(shù)a的取值范圍;
成立,求實數(shù)a的取值范圍; 在[0,1]上恰有兩個不同的實根,求實數(shù)b的取值范圍.
在[0,1]上恰有兩個不同的實根,求實數(shù)b的取值范圍. +4x+3,g(x)為一次函數(shù),若f(g(x))=x
+4x+3,g(x)為一次函數(shù),若f(g(x))=x +10x+24,求g(x)
+10x+24,求g(x)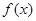 的定義域為
的定義域為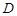 ,如果對于任意
,如果對于任意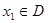 ,存在唯一
,存在唯一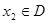 ,使
,使 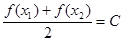 (
(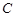 為常數(shù))成立,則稱
為常數(shù))成立,則稱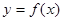 在
在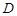 上的均值為
上的均值為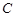 ,給出下列四個
,給出下列四個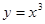 ;②
;②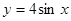 ;③
;③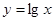 ;④
;④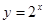 . 則滿足在其定義域上均值為2
. 則滿足在其定義域上均值為2