
利用某些已經證明的不等式,從________出發,運用不等式的________推出所要證的不等式,這種證明不等式的方法叫做綜合法.其思維特點是________,即從________逐步向________靠攏.
 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案科目:高中數學 來源: 題型:
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
| 13 |
| 24 |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
查看答案和解析>>
科目:高中數學 來源:2010年大連市高二下學期六月月考理科數學卷 題型:選擇題
利用數學歸納法證明“ ”的過程中,
”的過程中,
由“n=k”變到“n=k+1”時,不等式左邊的變化是 ( )
(A)增加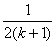 (B)增加
(B)增加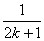 和
和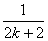
(C)增加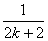 ,并減少
,并減少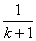 (D)增加
(D)增加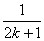 和
和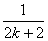 ,并減少
,并減少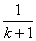
查看答案和解析>>
科目:高中數學 來源:2010年云南省昆明八中高考數學二模試卷(理科)(解析版) 題型:選擇題
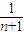 +
+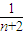 +…+
+…+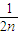 >
> (n>1且n∈N)時,在證明n=k+1這一步時,需要證明的不等式是( )
(n>1且n∈N)時,在證明n=k+1這一步時,需要證明的不等式是( )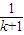 +
+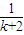 +…+
+…+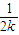 >
>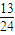
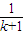 +
+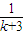 +…+
+…+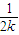 +
+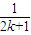 >
>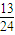
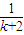 +
+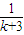 +…+
+…+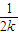 +
+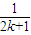 >
>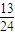
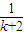 +
+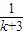 +…+
+…+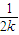 +
+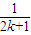 +
+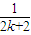 >
>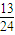
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省高三第五次質量檢測文科數學試卷(解析版) 題型:解答題
已知函數
(Ⅰ)若函數f(x)在[1,2]上是減函數,求實數a的取值范圍;
(Ⅱ)令g(x)= f(x)-x2,是否存在實數a,當x∈(0,e](e是自然常數)時,函數g(x)的最小值是3,若存在,求出a的值;若不存在,說明理由;
(Ⅲ)當x∈(0,e]時,證明:
【解析】本試題主要是考查了導數在研究函數中的運用。第一問中利用函數f(x)在[1,2]上是減函數,的導函數恒小于等于零,然后分離參數求解得到a的取值范圍。第二問中,
假設存在實數a,使 有最小值3,利用
有最小值3,利用 ,對a分類討論,進行求解得到a的值。
,對a分類討論,進行求解得到a的值。
第三問中,
因為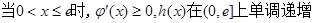 ,這樣利用單調性證明得到不等式成立。
,這樣利用單調性證明得到不等式成立。
解:(Ⅰ) 
(Ⅱ) 
(Ⅲ)見解析
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com