(1)圓C:x2+y2+Dx+Ey+F=0的外部有一點P(x,y),求由點P向圓引切線的長度;
(2)在直線2x+y+3=0上求一點P,使由P向圓x2+y2-4x=0引得的切線長度為最小.
【答案】
分析:(1)先把x
2+y
2+Dx+Ey+F=0,通過配方化為標準方程則,明確圓心和半徑.再利用圓外有一點P(x
,y
),由點P向圓引切線,切線長、半徑和PO組成直角三角形;再根據勾股定理求出切線長.
(2)已知圓x
2+y
2-4x=0求出圓心和半徑為.再根據圖形和幾何性質,要在直線2x+y+3=0上求一點P,使由P向圓x
2+y
2-4x=0引得的切線長度為最小.半徑已定,只需要滿足直線上一點到圓心的距離最小即可.顯然直線上一點P即為,過圓心與直線2x+y+3=0垂直的交點.
解答:解:(1)已知圓C:x
2+y
2+Dx+Ey+F=0,則,圓心為O為
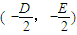
,半徑為
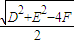
;
圓外有一點P(x
,y
),由點P向圓引切線,切線長、半徑和PO組成直角三角形;
根據勾股定理易得:切線長=
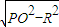
其中PO=
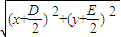
R=
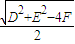
;
代入上式化簡為
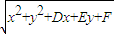
即為所求.
(2)已知圓x
2+y
2-4x=0.易得圓心為(2,0),半徑為2.
要在直線2x+y+3=0上求一點P,使由P向圓x
2+y
2-4x=0引得的切線長度為最小.
半徑已定,只需要滿足直線上一點到圓心的距離最小即可.
顯然直線上一點P即為,過圓心與直線2x+y+3=0垂直的交點.
該直線為:x-2y-2=0
聯立 2x+y+3=0
求得
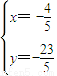
則該點P為(
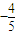
,
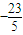
)即為所求.
答:(1)圓C:x
2+y
2+Dx+Ey+F=0的外部有一點P(x
,y
),點P向圓引切線的長度為
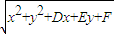
(2)直線2x+y+3=0上一點P為(
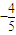
,
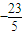
)P向圓x
2+y
2-4x=0引得的切線長度為最小.
點評:(1)圓C:x
2+y
2+Dx+Ey+F=0的外部有一點P(x
,y
),點P向圓引切線的長度為
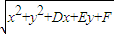
,可以把此當結論記住. (2)解決直線與圓的相關問題,盡量充分利用直線與圓的相關幾何性質加以解決.

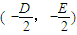 ,半徑為
,半徑為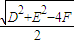 ;
;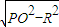
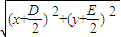
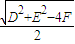 ;
;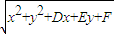
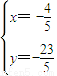
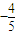 ,
,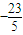 )即為所求.
)即為所求.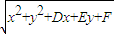
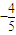 ,
,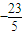 )P向圓x2+y2-4x=0引得的切線長度為最小.
)P向圓x2+y2-4x=0引得的切線長度為最小.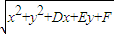 ,可以把此當結論記住. (2)解決直線與圓的相關問題,盡量充分利用直線與圓的相關幾何性質加以解決.
,可以把此當結論記住. (2)解決直線與圓的相關問題,盡量充分利用直線與圓的相關幾何性質加以解決. 

 閱讀快車系列答案
閱讀快車系列答案