
如圖,矩形ABCD中,|AB|=2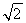 ,|BC|=2.E,F,G,H分別是矩形四條邊的中點,分別以HF,EG所在的直線為x軸,y軸建立平面直角坐標系,已知
,|BC|=2.E,F,G,H分別是矩形四條邊的中點,分別以HF,EG所在的直線為x軸,y軸建立平面直角坐標系,已知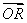 =λ
=λ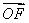 ,
,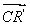 =λ
=λ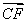 ,其中0<λ<1.
,其中0<λ<1.
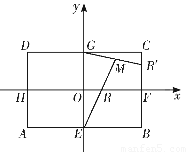
(1)求證:直線ER與GR′的交點M在橢圓Γ: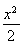 +y2=1上;
+y2=1上;
(2)若點N是直線l:y=x+2上且不在坐標軸上的任意一點,F1、F2分別為橢圓Γ的左、右焦點,直線NF1和NF2與橢圓Γ的交點分別為P、Q和S、T.是否存在點N,使得直線OP、OQ、OS、OT的斜率kOP、kOQ、kOS、kOT滿足kOP+kOQ+kOS+kOT=0?若存在,求出點N的坐標;若不存在,請說明理由.
(1)見解析(2)滿足條件的點N存在,其坐標為
【解析】
試題分析:根據條件,可用參數 表示點
表示點 的坐標,兩點式寫出直線
的坐標,兩點式寫出直線 的方程,并求出它們的交點
的方程,并求出它們的交點 的坐標,消去參數即可得證.(2)假設存在點
的坐標,消去參數即可得證.(2)假設存在點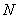 在直線
在直線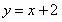 上,使
上,使 ,
,
設 ,
, ,
, ,
, ,
, 直線
直線 的斜率為
的斜率為 ,直線
,直線 的斜率為
的斜率為 ,可寫出兩直線的方程,并分別與橢圓方程聯立組成方程級,利用一元二次方程根與系數的關系,結合條件
,可寫出兩直線的方程,并分別與橢圓方程聯立組成方程級,利用一元二次方程根與系數的關系,結合條件 探究
探究 與
與 的關系,從而確定關于
的關系,從而確定關于 的方程的根的存在性,也就是點
的方程的根的存在性,也就是點 的存在性.
的存在性.
試題解析:(1)由已知,得F( ,0),C(
,0),C( ,1).
,1).
由 =λ
=λ ,
, =λ
=λ ,得R(
,得R( λ,0),R′(
λ,0),R′( ,1-λ).
,1-λ).
又E(0,-1),G(0,1),則
直線ER的方程為y=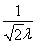 x-1, ①
x-1, ①
直線GR′的方程為y=- x+1. ②
x+1. ②
由①②,得M( ,
, ).
).
∵ +(
+( )2=
)2= =
= =1,
=1,
∴直線ER與GR′的交點M在橢圓Γ: +y2=1上. 5分
+y2=1上. 5分
(2)假設滿足條件的點N(x0,y0)存在,則
直線NF1的方程為y=k1(x+1),其中k1= ,
,
直線NF2的方程為y=k2(x-1),其中k2= .
.
由消去y并化簡,得(2k12+1)x2+4k12x+2k12-2=0.
設P(x1,y1),Q(x2,y2),則x1+x2=- ,x1x2=
,x1x2= .
.
∵OP,OQ的斜率存在,∴x1≠0,x2≠0,∴k12≠1.
∴kOP+kOQ= +
+ =
= +
+ =2k1+k1·
=2k1+k1· =k1(2-
=k1(2- )=-
)=- .
.
同理可得kOS+kOT=- .
.
∴kOP+kOQ+kOS+kOT=-2( +
+ )=-2·
)=-2· =-
=- .
.
∵kOP+kOQ+kOS+kOT=0,∴- =0,即(k1+k2)(k1k2-1)=0.
=0,即(k1+k2)(k1k2-1)=0.
由點N不在坐標軸上,知k1+k2≠0,
∴k1k2=1,即 ·
· =1. ③
=1. ③
又y0=x0+2, ④
解③④,得x0=- ,y0=
,y0= .
.
故滿足條件的點N存在,其坐標為(- ,
, ). 13分
). 13分
考點:1、動點軌跡方程的求法;2、直線與橢圓的位置關系的應用;3、平面向量的坐標表示.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
 如圖,矩形ABCD中,AB=
如圖,矩形ABCD中,AB=8
| ||
| 3 |
| 2π |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 A 若方程ax-x-a=0有兩個實數解,則a的取值范圍是
A 若方程ax-x-a=0有兩個實數解,則a的取值范圍是| AE |
| AF |
| 9 |
| 2 |
| 9 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,矩形ABCD中,DC=
如圖,矩形ABCD中,DC=| 3 |
2
| ||||
| 12 |
2
| ||||
| 12 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (理)如圖,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD
(理)如圖,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD| PQ |
| QD |
| BP |
| QD |
| ||
| 10 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com