【題目】已知橢圓C：
過點
，左焦點
（1）求橢圓C的標準方程；
（2）過點F作于x軸不重合的直線l，l與橢圓交于A，B兩點，點A在直線
上的投影N與點B的連線交x軸于D點，D點的橫坐標
是否為定值?若是，請求出定值；若不是，請說明理由
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】為了解某地區的“微信健步走”活動情況,現用分層抽樣的方法從中抽取老、中、青三個年齡段人員進行問卷調查.已知抽取的樣本同時滿足以下三個條件:
（i）老年人的人數多于中年人的人數;
（ii）中年人的人數多于青年人的人數;
（iii）青年人的人數的兩倍多于老年人的人數.
①若青年人的人數為4,則中年人的人數的最大值為___________.
②抽取的總人數的最小值為__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
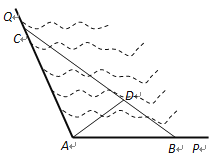
【題目】如圖所示，
是某海灣旅游區的一角，其中
，為了營造更加優美的旅游環境，旅游區管委會決定在直線海岸
和
上分別修建觀光長廊
和AC，其中是寬長廊，造價是
元/米，
是窄長廊，造價是
元/米，兩段長廊的總造價為120萬元，同時在線段
上靠近點
的三等分點
處建一個觀光平臺，并建水上直線通道
（平臺大小忽略不計），水上通道的造價是
元/米．
(1) 若規劃在三角形
區域內開發水上游樂項目，要求
的面積最大，那么和的長度分別為多少米？
(2) 在(1)的條件下，建直線通道還需要多少錢？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左、右兩個焦點分別為
，P是橢圓上位于第一象限內的點，
軸，垂足為Q，
，
，
的面積為
.
（1）求橢圓F的方程：
（2）若M是橢圓上的動點，求
的最大值，并求出取得最大值時M的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知正方體
的棱長為2，E、F、G分別為
的中點，給出下列命題：
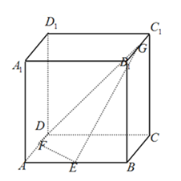
①異面直線EF與AG所成的角的余弦值為
；
②過點E、F、G作正方體的截面，所得的截面的面積是
；
③
平面
④三棱錐
的體積為1
其中正確的命題是_____________（填寫所有正確的序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，點
滿足方程
.
（1）求點M的軌跡C的方程；
（2）作曲線C關于
軸對稱的曲線，記為
，在曲線C上任取一點
，過點P作曲線C的切線l，若切線l與曲線交于A，B兩點，過點A，B分別作曲線的切線
，
，且，的交點為Q，試問以Q為直角的
是否存在，若存在，求出點P的坐標；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】人們常說的“幸福感指數”就是指某個人主觀地評價他對自己目前生活狀態的滿意程度的指標，常用區間
內的一個數來表示，該數越接近
表示滿意度越高．為了解某地區居民的幸福感情況，隨機對該地區的男、女居民各
人進行了調查，調查數據如表所示：
幸福感指數 |
|
|
|
|
|
男居民人數 |
|
|
|
|
|
女居民人數 |
|
|
|
|
|
（1）估算該地區居民幸福感指數的平均值；
（2）若居民幸福感指數不小于
，則認為其幸福．為了進一步了解居民的幸福滿意度，調查組又在該地區隨機抽取
對夫妻進行調查，用
表示他們之中幸福夫妻（夫妻二人都感到幸福）的對數，求的期望（以樣本的頻率作為總體的概率）.
查看答案和解析>>
科目：高中數學 來源： 題型：
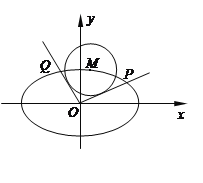
【題目】如圖，在平面直角坐標系
中，設點
是橢圓
上一點，從原點
向圓
作兩條切線分別與橢圓
交于點
，直線
的斜率分別記為
．
（1）若圓
與
軸相切于橢圓的右焦點，求圓的方程；
（2）若
．
①求證：
；
②求
的最大值
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知兩個集合A，B，滿足BA．若對任意的x∈A，存在ai，aj∈B（i≠j），
使得x=λ1ai+λ2aj（λ1，λ2∈{﹣1，0，1}），則稱B為A的一個基集．若A={1，2，3，4，5，6，7，8，9，10}，則其基集B元素個數的最小值是__
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
